【中学1年数学（正の数・負の数）】プラスとマイナスの計算の意味 – 足し算と引き算はこう考えよう
- 「正の数・負の数」の計算がわからない
- 特に、負の数の引き算がわからない
- プラスとマイナスの計算のイメージが湧かない
中学生になって始めに学ぶ、「正の数・負の数」では負の数の計算が”やっかい”です。
なぜ、マイナスとマイナスが続いていると（\(1-(-1)\)）、足し算と同じ（\(1+1\)）になるのでしょうか？
はじめは頭が混乱するかもしれませんね。
こんな計算を理解するには、矢印をイメージすると”なぜそんな計算になるのか”ということがわかります。
ここでは、正の数・負の数の計算を頭の中でしっかりイメージして理解してもらうことを目的にしています。
プラスとマイナスの計算の意味が”やっかい”なのはイメージがないから
中学1年生で習う”正の数と負の数”では、プラスとマイナスの数を足し算や引き算する計算が登場します。
ここやっかいなのが、負の数（マイナス）の数の計算です。
なぜやっかいなのか？
それは、
負の数が日常生活では、イメージしづらい
という点にすべての原因があると思っています。
正の数（プラス）であれば、日常生活に毎日登場します。
例えば、
「あなたはペンを何本持っていますか？」
「欲しいお菓子を買うのにいくら必要ですか？」
このような質問にあなたは、正の数で答えると思います。
まさか、「わたしはマイナス3本のシャーペンを持っている」とは答えないでしょう。
このように、負の数の計算が難しく感じるのは、負の数のイメージがないからなのです。
スポンサーリンク
正の数と負の数は数直線上の矢印と考えよう
負の数のイメージがないから計算が難しいということは、逆に言えばイメージさえ持ってしまえば、簡単に計算できるようになるということです。
そこで、正の数・負の数のイメージを次のように考えましょう。
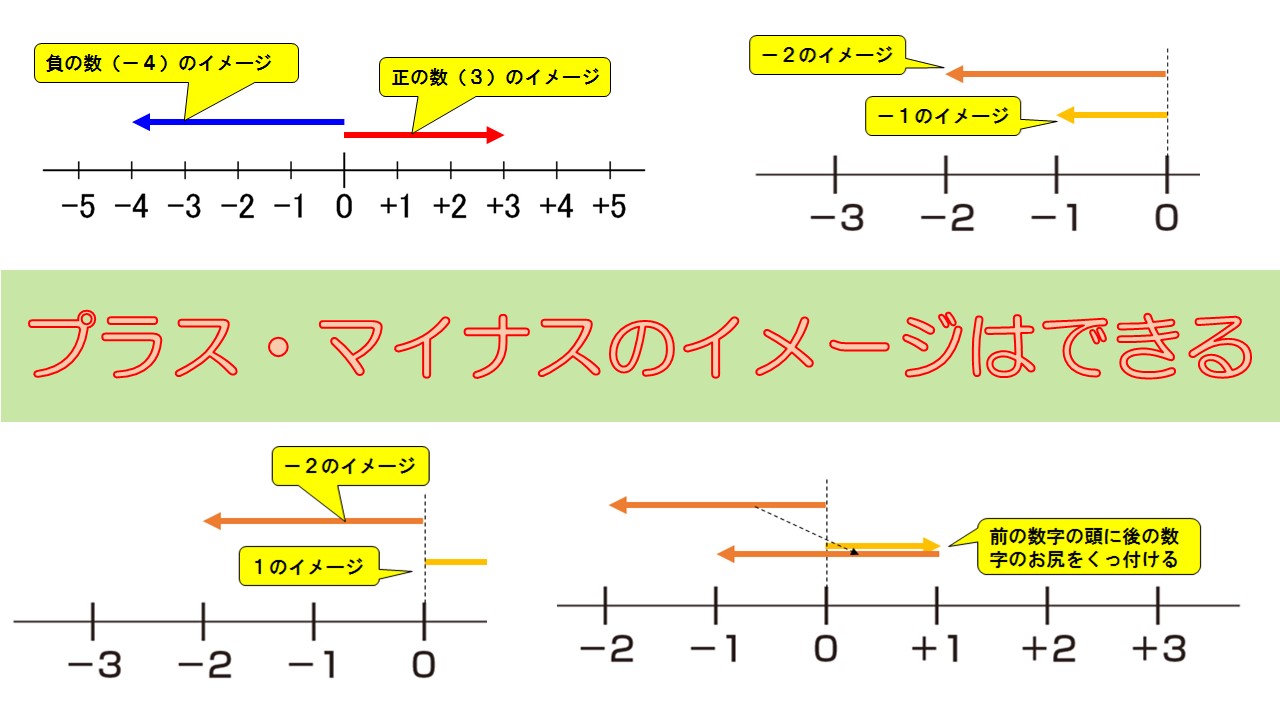
- 正の数は、数直線上の右向きの矢印
- 負の数は、数直線上の左向きの矢印
これから、何か数字を考えるとき、このような矢印でイメージするようにしましょう。
私たちの生活に登場する数字は、正の数と負の数しかありませんから、すべての数字がこのような矢印でイメージできるはずです。
矢印を使って足し算と引き算を解く
さて、このイメージができるようになったら次は、正の数と負の数が登場する足し算と引き算を解いていきましょう。
正の数と負の数を使った計算にどんな計算パターンがあるのかを確認します。
足し算を計算する
まずは、足し算ですが、次の4つパターンがあります。
\begin{align}
& 1 + 2 \\
& 1 + (-2) \\
& (-1) + 2 \\
& (-1) + (-2)
\end{align}
\(1+2\)
一番上のパターンは正の数同士（\(1\)と\(2\)）の足し算です。
$$1+2$$
これを矢印をイメージして解いてみましょう。
まずは、それぞれの数字を数直線上に矢印で描きます。
うまくイメージできましたか？
次に足し算の計算です。
足し算は、二つの矢印を足すと考えます。
二つの矢印を足すときは、前の数字（ここでは\(1\)）の矢印の頭に、後の数字（ここでは\(2\)）の矢印のお尻をくっつけます。
すると、二つを足した矢印の長さは\(+3\)となっていることがわかりますね。
なので、この足し算の答えは、
$$1 + 2 = 3$$
となるのです。
「こんな簡単な計算はわざわざこんな面倒なことしなくても分かる」
と思うかもしれません。
しかし、ここで重要なことは、矢印をイメージして計算ができるかどうかです。
簡単な問題で、イメージする練習をしておきましょう。
そうすることで、もっと複雑な計算がでてきても抵抗無くイメージでき、計算できるようになりますよ。
\(1 + (-2)\)
次は、後の数字が負の数の計算ですね。
これも矢印をイメージできれば、\(1+2\)と同じように計算できます。
下の図のように矢印をイメージしましょう。
\(-2\)は負の数なので、矢印の向きが逆になります。ここがきちんとイメージできていればオッケーです。
次は、矢印を足しましょう。
前の数字（ここでは\(1\)）の矢印の頭に、後の数字（ここでは\(-2\)）の矢印のお尻をくっつけます。
すると、二つを足したあとの矢印を先はどこにあるでしょうか？
\(-1\)のところにありますね。よって、答えは\(-1\)となるのです。
$$1+(-2) = -1$$
\((-1)+2\)
次は、前の数字（\(-1\)）が負の数の場合です。
この場合も計算イメージは同じです。矢印は以下のようになりますね。
そして、前の数字（ここでは\(-1\)）の矢印の頭に、後の数字（ここでは\(2\)）の矢印のお尻をくっつけます。
二つを足した後の矢印の先は\(1\)にあります。答えは\(1\)です。
$$(-1)+2 = 1$$
\((-1)+(-2)\)
最後は、二つの数字が負の数の場合ですね。
これも今までと同じように考えればオッケーです。
まずは、矢印のイメージです。
そして、前の数字（ここでは\(-1\)）の矢印の頭に、後の数字（ここでは\(-2\)）の矢印のお尻をくっつけます。
答えは、\(-3\)ですね。
$$(-1)+(-2) = -3$$
足し算のまとめ
これで、すべての足し算のパターンを見てきました。
パターンに分けて説明しましたが、計算の方法はどれも一緒だったということに注目してくださいね。
- 足し算の式に登場する矢印を数直線上にイメージする
- 前の数字の矢印の頭に、後の数字の矢印のお尻をくっつける
- 最終的な矢印の先が示している数が答えとなる
引き算を計算する
まずは、引き算ですが、次の4つパターンがあります。
\begin{align}
& 1 – 2 \\
& 1 – (-2) \\
& (-1) – 2 \\
& (-1) – (-2)
\end{align}
引き算の場合は、足し算の考え方にひと手間加えるだけです。
以下で実際に計算しながら、一つずつ順番に考えていきましょう。
\(1-2\)
$$1-2$$
の計算です。
まずは、足し算のときと同じように、使われている数（\(1\)と\(2\)）を数直線上に矢印として表示してみましょう。
となります。
これは問題ないですね。足し算のときとまったく一緒です。
次に、引き算であることを思い出します。そして、
引き算の場合は、引く数（ここでは\(2\)）の矢印を逆
に向けます。
この作業が足し算と違う点です。
あとは、足し算のときと同じく、前の数字（ここでは\(1\)）の矢印の頭に、後の数字（ここでは\(2\)）の矢印のお尻をくっつけます。
最後の矢印の先が\(-1\)となっていますね。答えは\(-1\)です。
$$1 – 2 = -1$$
これが引き算の基本的な解き方です。
これから残りの3つのパターンの引き算についても紹介しますが、どれもまったく同じ解き方ですべて解けます。
足し算のときとほとんど同じですが、忘れてはいけないのは引き算の場合は引く数の矢印を始めに逆にするということです。
\(1-(-2)\)
今度は、マイナスが二つ連続していますね。
難しそうですが、大丈夫です。落ち着いて今まで通り進めていけば確実に解けます。
まず、引き算に使われている2つの数を矢印にしましょう。
そして、引き算ですので、引く数（\(-2\)）の矢印を逆にします。
最後に、前の数字の矢印の頭に、後の数字の矢印のお尻をくっつけて終わりですね。
最後の矢印の先の位置は\(3\)です。よって、
$$1-(-2) = 3$$
ですね。
\((-1)-2\)
次は、前の数（\(-1\)）が負の数になっています。
同じようにして解いてみましょう。
まずは、2つの数の矢印ですね。
次に、引き算なので、引く数（\(2\)）の矢印の反転です。
最後に、前の数字の矢印の頭に、後の数字の矢印のお尻をくっつけて終わりですね。
最後の矢印の先の位置は\(-3\)です。よって、
$$(-1)-2 = -3$$
ですね。
\((-1)-(-2)\)
最後は負の数同士の引き算です。
マイナス記号がたくさん登場して混乱してしまいそうですが、同じようにしてゆっくり確認しながら解けば大丈夫です。
まずは、2つの数の矢印ですね。
次に、引き算なので、引く数（\(-2\)）の矢印の反転です。
そして最後に、前の数字の矢印の頭に、後の数字の矢印のお尻をくっつけて終わりですね。
最後の矢印の先の位置は\(1\)です。よって、
$$(-1)-(-2) = 1$$
ですね。
スポンサーリンク
まとめ
これで、正の数・負の数のすべての計算パターンを見てきました。
すべての計算に共通することは、数字を矢印でイメージすることと、矢印をつなげて最終的な矢印の先端が答えであるということです。
ただし、引き算の場合は、つなげる前に矢印を反転しましょう。
これができれば、どんな計算も必ず混乱せずできます。
あとは、いろんな問題を解いて慣れるだけです。