【中学2年数学（式の計算）】同類項とは – 同類項をまとめると計算ができる
- 同類項とは何かがわからない人
- 同類項の探し方・見分け方がわからない人
- 同類項を知ることで、どのようなメリット（良いこと）があるのか知りたい人
ここでは、「同類項とは何か？」や「同類項の探し方」を解説しています。
このページを読めば、もう同類項を探し出すことで悩んだりしなくなるはずです。
また、同類項がわかると何かよいことがあるのでしょうか？
実は、文字の式の計算は、同類項を知ることから始まるのです。
このような、同類項を知ることによるメリットについても紹介していきましょう。
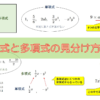
同類項とは
同類項とは、
1つの多項式で、文字の部分が同じである項
のことです。
ここで、多項式という言葉が登場しました。
多項式とは、”引き算や足し算が使われている式”のことです。
$$7x^2-x+7, \quad a^3-5ab-7b^2$$
詳しくは、以下のページをご覧ください。
https://analytics-notty.tech/what-are-monomials-and-polynomials/
さて、同類項である”1つの多項式で、文字の部分が同じである項”というのは、いったいどういうことでしょうか。
例として、次の式を見てください。
$$4x+3y-5x+2y$$
この式で文字の部分が同じ項はどこでしょう。
項というのは、式を作っている一つ一つの単項式のことです（下の図を参照）。
まず、この多項式を単項式に分解しましょう。
すると、
$$4x, \quad 3y, \quad -5x, \quad 2y$$
と4つの項（単項式）から作られていることがわかります。
文字の種類は\(x\)と\(y\)の二つがありますね。
\(x\)が使われている項は、
$$4x, \quad -5x$$
の2つです。
この2つを同類項と呼びます。
\(4x\)と\(-5x\)は同類項
この式には、もう一組だけ同類項があります。
それは、\(3y\)と\(2y\)ですね。
同じ文字\(y\)が使われているからです。
\(3y\)と\(2y\)は同類項
文字が同じでも、次数が違えば同類項ではない
ここで一つ注意点があります。
例えば、以下の式をみてください。
$$x^2 + 2x + 1$$
この多項式の同類項はどれでしょうか？
同じ文字\(x\)が使われているのは、\(x^2\)と\(2x\)の項です。
この二つは、同類項でしょうか？
いいえ、この二つは同類項ではありません。
\(x^2\)と\(2x\)は同類項ではない
それは、次数が違うからです。
\(x^2\)の次数は\(2\)であるのに対して、\(2x\)の次数は\(1\)ですね。
このように、同じ\(x\)を使った項でも、次数が違えば同類項とはいえないのです。
ここまでをまとめましょう。
同類項とは、同じ文字を使った項同士のことをいいます。
\(2x\)と\(\frac{3}{4}x\)は同類項
しかし、同じ文字でも次数が違えば同類項にはなりません。
\(x\)と\(x^2\)は同類項ではない
練習してみよう
同類項の見分け方はわかりましたか？
「わかった！」という人は、次の問題に挑戦してみましょう。
$$ab + a^2 – \frac{1}{2}a + 6a^2 – ab^2$$
の式の同類項を答えなさい。
解いてみます。
まず、問題の多項式、
$$ab + a^2 – \frac{1}{2}a + 6a^2 – ab^2$$
を項（単項式）に分解しましょう。
すると、
$$ab, \quad a^2, \quad -\frac{1}{2}a, \quad 6a^2, \quad -ab^2$$
ですね。
この中で、使われている文字が同じで、次数も同じものを選べばよいです。
それは、\(a^2\)と\(-\frac{1}{2}a\)ですね。
この2つが同類項です。
解けましたか？
スポンサーリンク
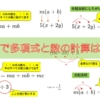
同類項同士は計算ができる
ここまで、同類項の見つけ方を学んできました。
しかし、同類項を見つけれるようになると、何がいいのでしょうか？メリットは何でしょうか？
それは、
計算できる項がわかる
ということです。
文字を含んだ式を計算するとき、
同類項どうしは計算ができる
のです。
次の式をみてください。
$$x^2 + x – 3x^2 + 4$$
この式の中で、同類項は、
\(x^2\)と\(-3x^2\)
ですね。
ということは、この2つの項どうしは計算ができます。
この2つの項の計算は、次のようになります。
$$x^2 – 3x^2 = (1-3) x^2 = -2 x^2$$
このように、同類項の計算では、共通している文字の部分はそのままにし、文字の係数部分だけを計算します。
すると、元の式（\(x^2 + x – 3x^2 + 4\)）は、
$$x^2 + x – 3x^2 + 4 = -2x^2 + x + 4$$
となります。
これで計算は終わりです。
この式に同類項はもうありませんね。
同類項がなければ計算はできないのです。
\(-2x^2\)と\(x\)は同類項ではないということに注意してください。
同じ文字\(x\)が使われてはいますが、次数が違うからです。
よって、\(-2x^2\)と\(x\)は計算はできないのです。
まとめ
ここでは、同類項とは何なのか？や同類項の見つけ方を学んできました。
また、同類項がわかると何がうれしいのかもわかってもらえたのではないでしょうか？
ここで学んだことは、今後、文字の式の計算を行っていく上で、非常に大切なことなのでわからないところはしっかりと復習しておきましょうね。
では、最後に重要ポイントを復習して終わりましょう。
同類項とは、多項式の中で文字の部分が同じである項をいう。
※文字の種類だけでなく、次数も同じである必要がある。
同類項同士は計算が可能である。
逆に、同類項でなければ、計算はできないことに注意。
それでは、お疲れ様でした。