【中学2年数学(式の計算)】多項式と数の乗法(掛け算)・除法(割り算) – 分配法則を使って計算しよう

- 多項式の掛け算や割り算のやり方がわからない
- 多項式に分配法則を使って計算する方法が知りたい
- 多項式を解く計算手順を復習したい
このページでは、多項式と数の乗法(掛け算)と除法(割り算)の計算方法を紹介しています。
次のような式の計算です。
\begin{align}
& 5 (x + 2y) \\
& 5 (x + 2y + 3z) \\
& (6a – 3b) \div 3
\end{align}
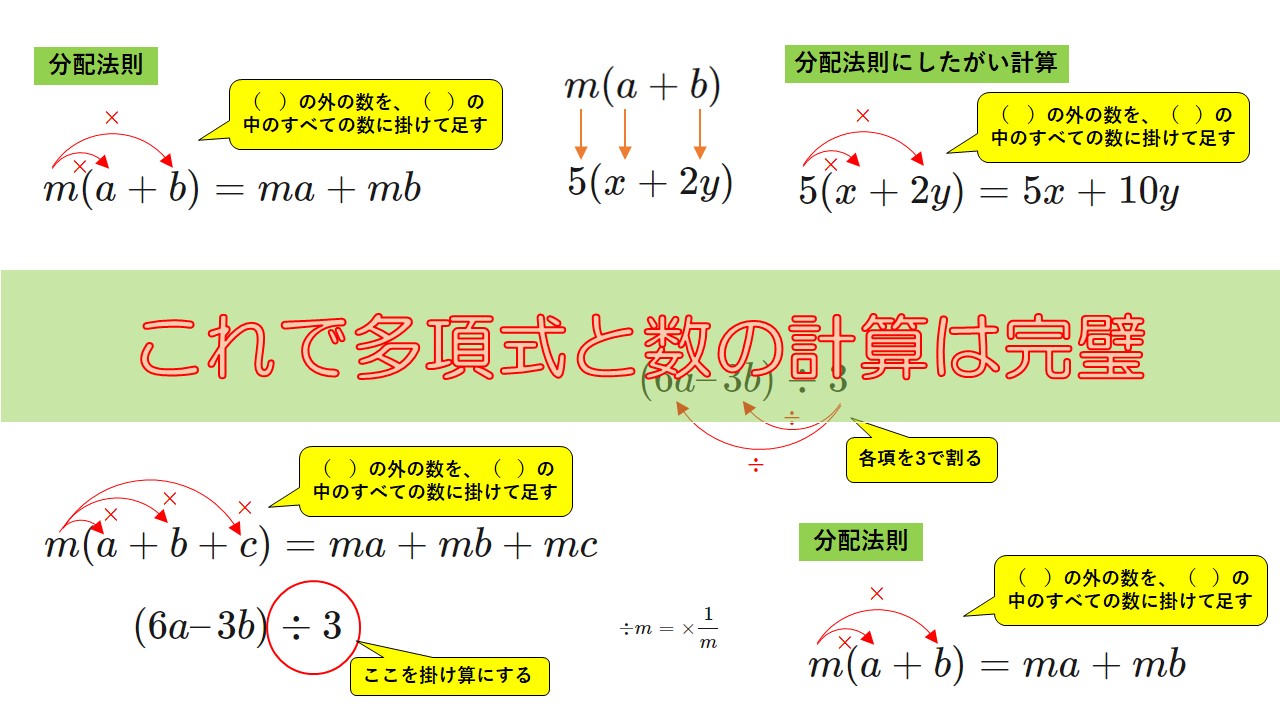
これらの式は分配法則を使って計算します。
このページを読み終わるころには、これらの計算はスラスラ解けるようになっているはずですよ。
それでは、はじめましょう。
多項式と数の乗法(掛け算)は分配法則を使って求めよう
まずは、次のような式の計算を解く方法を紹介しましょう。
$$5 (x + 2y)$$
この式は、多項式である\((x+2y)\)と数である\(5\)が掛けられていますね。
このような計算をする場合、分配法則を使います。
分配法則とは、
$$m (a + b) = ma + mb$$
という計算です。
数\(m\)を多項式の各項で(\(a\)と\(b\))にそれぞれに掛けたものを足しています。

\(m\)を\(a\)と\(b\)に分配していますね。
だから、分配法則です。
では、この分配法則の公式を使って、先ほどの、
$$5 (x + 2y)$$
を計算してみましょう。
( )の外の\(5\)が上の分配法則の公式の\(m\)の部分にあたりますね。
また、( )の中の\(x\)と\(2y\)が公式の\(a\)と\(b\)になります。
\begin{align}
m & \rightarrow 5 \\
a & \rightarrow x \\
b & \rightarrow 2y
\end{align}
よって、公式にあてはめ計算すると、
\begin{align}
5 (x + 2y) & = 5 \times x + 5 \times 2y \\
& = 5x + 10y
\end{align}
となります。

よって、\(5 (x + 2y)\)の答えは、\(5x + 10y\)です。
かっこの中の項数(項の数)が増えた場合
では、次の問題はどうでしょうか?
$$5 (x + 2y + 3z)$$
( )の中の項の数が三つになりました。
このようなときも、( )の外の数を、( )の中の各項にそれぞれ掛け算します。
つまり、
$$m (a + b + c) = ma + mb + mc$$
という分配法則が成り立ちます。
これを使って、計算問題を解くと、
\begin{align}
5 (x + 2y + 3z) & = 5 \times x + 5 \times 2y + 5 \times 3z \\
& = 5x + 10y + 15z
\end{align}
となります。
さらに、項の数が増えても一緒です。
( )の外の数を、( )の中の項に一つ一つ掛けて、足せばオッケーです。
スポンサーリンク
多項式と数の除法(割り算)も同じ方法で計算できる
続いて、割り算の場合を紹介しましょう。
次のような計算です。
$$(6a – 3b) \div 3$$
掛け算のときは( )の外の数を( )の中の項に掛けました。

割り算のときは( )の外の数で( )の中の項を割ります。
つまり、割り算のときの分配法則は、
\begin{align}
(a + b) \div m & = a \div m + b \div m \\
& = \frac{a}{m} + \frac{b}{m}
\end{align}
となります。

上の計算式、
$$(6a – 3b) \div 3$$
に公式を使って、計算してみましょう。
( )の外の\(3\)で、( )の中の\(6a\)と\(-3b\)を割って足せばよいですね。
\begin{align}
6a \div 3 & = 2a \\
-3b \div 3 & = -b
\end{align}
なので、
\begin{align}
(6a – 3b) \div 3 & = 2a + (-b)\\
& = 2a – b
\end{align}
となります。
答えは、\(2a-b\)です。
かっこの中の項数(項の数)が増えた場合
割り算の場合も、( )の中の項の数が増えても同様にして解けばオッケーです。
例えば、
$$(-9x + 15y + 6) \div 3$$
という問題を解いてみましょう。
( )の外の数で、( )の中の各項をそれぞれ割ります。
\begin{align}
-9x \div 3 & = -3x \\
15y \div 3 & = 5y \\
6 \div 3 & = 2
\end{align}
であり、これらを最後にすべて足して、
\begin{align}
(-9x + 15y + 6) \div 3 = -3x + 5y + 2
\end{align}
となります。
割り算を掛け算に変形して計算する方法
次に、多項式と数の除法(割り算)の別の解き方を紹介します。
それは、
割り算を掛け算に変形して計算する
という方法です。
実際にやってみましょう。
$$(6a – 3b) \div 3$$
を例として説明します。
最後の\(\div 3\)に注目してください。
少し考え方を変えて、”\(\div 3\)”を”\(\times \frac{1}{3}\)”とします。
$$\div 3= \times \frac{1}{3}$$
すると、問題の式は、
\begin{align}
(6a – 3b) \div 3 & = (6a – 3b) \times \frac{1}{3} \\
& = \frac{1}{3} (6a – 3b)
\end{align}
と変形できます。
これで、掛け算の分配法則が使えるようになりました。

\((6a-3b)\)のそれぞれの項へ\(\frac{1}{3}\)を掛けると、
\begin{align}
\frac{1}{3} \times 6a & = \frac{6a}{3} = 2a \\
\frac{1}{3} \times (-3b) & = \frac{-3b}{3} = -b
\end{align}
なので、答えは、
\begin{align}
(6a – 3b) \div 3 & = 2a + (-b) \\
& = 2a – b
\end{align}
となります。
これが、割り算を掛け算に変形して計算する方法です。
前の説明では、掛け算の分配法則を、
\begin{align}
m \times (a + b) = m \times a + m \times b
\end{align}
とし、割り算の分配法則を、
\begin{align}
(a + b) \div m = a \div m + b \div m
\end{align}
と別々に紹介して、問題によって使い分けるよう説明しました。。
しかし、ここで学んだ割り算を掛け算に変形する方法を使うならば、掛け算の分配法則だけ覚えておけば、オッケーなのです。
この計算方法は私のオススメの方法です。
割り算を掛け算に変形する方法を覚えておこう
割り算を掛け算に変形する方法で、重要なのは、割り算と掛け算に変形するとき、
$$\div m = \times \frac{1}{m}$$
となることです。
割り算から掛け算になると、整数は分数になってしまうのですね。
これをしっかり覚えておきましょう。
この変形が正しいことを調べるには、実際に計算してみるとよいでしょう。
例えば、\(m\)が\(5\)の場合は、
$$\div 5 = \times \frac{1}{5}$$
となります。
例えば、\(15\)に対して、上の式を使ってみると、
$$15 \div 5 = 15 \times \frac{1}{5}$$
となりますが、
\begin{align}
\text{左辺} & = 15 \div 5 = 3 \\
\text{右辺} & = 15 \times \frac{1}{5} = \frac{15}{5} = 3
\end{align}
であり同じになることがわかりますね。
まとめ
多項式と数の乗法(掛け算)と除法(割り算)の計算を説明しました。
どちらも分配法則を使って計算するので、分配法則が不安な人は、まずは、分配法則をしっかりと理解しましょう。
割り算の分配法則は、無理に覚えなくてもよいです。
割り算は掛け算に変形することができますので、始めに掛け算の式に変形してしまえば、あとは掛け算の分配法則を使って解いてしまいましょう。
では、最後に重要ポイントのおさらいをして終わります。
多項式と数の乗法(掛け算)と除法(割り算)の計算は、分配法則を使って解く。
掛け算の分配法則は、
$$m (a + b) = ma + mb$$
である。
割り算は掛け算に変形することができるので、最初の問題が割り算だったら、掛け算に変えてしまう。
$$\text{例:} (3a + 6) \div 3= (3a + 6) \times \frac{1}{3}$$
そうすることで、掛け算の分配法則だけを覚えて使えばよい。
最後まで読んでくれてありがとう。またね~。


























ディスカッション
コメント一覧
まだ、コメントがありません