分母が違う分数の足し算 – 通分して計算する理由は分配法則を考えればわかる!

- 分数の計算が苦手
- 分数の足し算はできるけど、どうして通分するのか理由が分からない
- 通分するときとしないときの区別がつかない
このページは、以下のような”分母が違う分数の足し算”の計算ができるようになることを目的としています。
$$\frac{1}{2} + \frac{1}{3} =$$
そのために、まずかけ算の分配法則(ぶんぱいほうそく)の仕組みを解説します。
分数の計算を、かけ算の分配法則を使って教える人はあまり見かけません。
何の関係があるのか疑問に思う人もいるかも知れませんが、じつは通分とかけ算の分配法則は強く関係しています。
このページを読んでもらえれば、分数の足し算の時に通分する理由が分かると思いますし、それさえ分かってしまえば、分数の足し算でつまずくこともなくなるはずです。
この記事で伝えたいことは、
分母が違う分数の足し算を通分して計算する理由は、分配法則を考えれば分かる
ということです。
はじめに、”分配法則”を知らない人・忘れた人へ向けて復習しますが、「もう、分配法則なんで知っている」という人は、「分母が違う分数の足し算を通分して計算する理由」から読みはじめてください。
まずはかけ算の分配法則をおさらいしよう
中学生の皆さんは、すでにかけ算の分配法則(ぶんぱいほうそく)を習っていると思います。
これは小学校で教えているからです。
ただ、名前は教わっていないかも知れません。
$$2 \times (3+4) = 2 \times 3 + 2 \times 4 = 6 + 8 = 14$$
こういう感じの計算は教わったことがあると思います。
この、
$$2 \times (3+4) = 2 \times 3 + 2 \times 4$$
というのが、かけ算の分配法則です。
ここでは、かけ算の分配法則が、具体的にはどんな法則なのか、もう少しかみ砕いてみましょう。
スポンサーリンク
かけ算の分配法則の意味
まずは、
$$2 \times 3 + 2 \times 4$$
という式に注目してください。
大事なことは、\(2\)が二回登場していることです。\(3\)も\(4\)も、\(2\)に対して掛けられています。
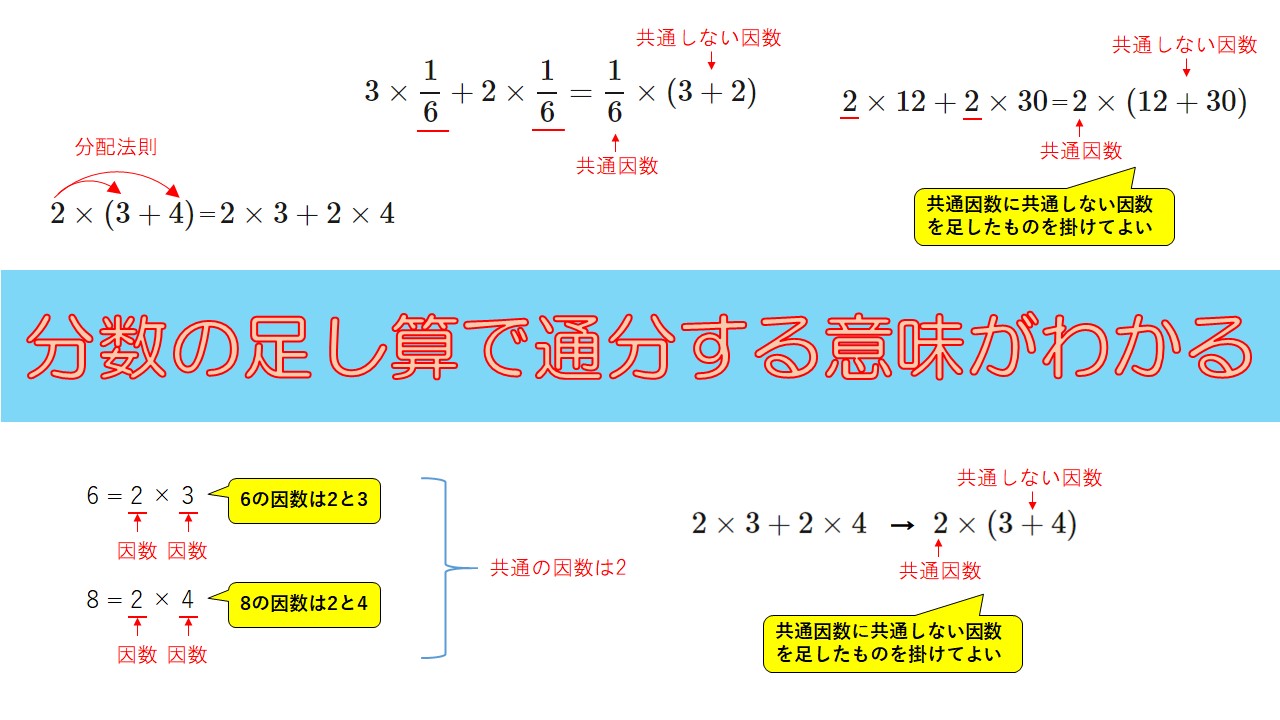
ということはつまり、\(2 \times 3\)と\(2 \times 4\)は共に、\(2\)という共通した因数を持っていることになります。
因数とは、かけ算の式の時に現れる、一つ一つの数や式のことを指します。
この場合なら\(2 \times 3\)の因数は\(2\)と\(3\)であり、\(2 \times 4\)の因数は\(2\)と\(4\)です。
そして、かけ算の分配法則は、
$$2 \times 3 + 2 \times 4=2 \times (3+4)$$
と定めているわけです。
これを日本語で表現すると、
共通する因数を持つ数を足しあわせるとき、かっこの中で、共通しない因数同士を足しあわせ、それを共通する因数にかけてもよい
となります。
\(2 \times 3\)と\(2 \times 4\)は\(2\)という共通する因数を持っています。
\(2 \times 3\)と\(2 \times 4\)を足しあわせるときは、かっこの中で、共通しない因数である\(3\)と\(4\)を足しあわせ、これを共通因数である\(2\)に掛けてもよい、ということになります。
「ほんとかぁ?」
「そういう計算が成り立つ場合もあるかも知れないけど、成り立たない場合もあるんじゃないのぉ?」
という疑問があるかも知れません。
もうちょっと、いろんなパターンを調べてみましょう。
$$2 \times 3 \times 4 + 2 \times 5 \times 6$$
の場合はどうなるでしょうか?
\(2 \times 3 \times 4\)の因数は\(2\)と\(3\)と\(4\)ですね。
\(2 \times 5 \times 6\)の因数は\(2\)と\(5\)と\(6\)です。
共通する因数は\(2\)だけですから、かけ算の分配法則を使うとこうなります。
$$2 \times 3 \times 4+2 \times 5 \times 6=2 \times (3 \times 4+5 \times 6) = 2 \times (12+30)$$
ここで注意してほしいのは、\(2 \times (3+4+5+6)\)ではないことです。
確かに私は、「かっこの中で、共通しない因数同士を足しあわせる」と書きました。
\(3\),\(4\),\(5\),\(6\)が共通しないのだから、これ全部足すんじゃないの?と思われるかも知れません。
しかし、
\begin{align}
2 \times 3 \times 4=2 \times 12 \\
2 \times 5 \times 6=2 \times 30
\end{align}
ですよね。
ということは、
$$2 \times 3 \times 4 + 2 \times 5 \times 6=2 \times 12 + 2 \times 30$$
でもあるはずです。
当然ながら、
$$2 \times 12+2 \times 30=2 \times (12+30)$$
でなければなりません。

かっこの外に出した共通因数以外は元の形のまま、かっこの中に入れてください。
ではもう一つ。
$$2 \times 3 \times 4 + 2 \times 3 \times 5$$
の場合はどうなるでしょうか?
\(2 \times 3 \times 4\)の因数は、\(2\),\(3\),\(4\)です。
\(2 \times 3 \times 5\)の因数は、\(2\),\(3\),\(5\)ですね。
ということは、共通因数は\(2\)と\(3\)の二つになります。
この場合はどうしたらいいのか?
やり方は一緒です。
$$2 \times 3 \times 4 + 2 \times 3 \times 5 = 2 \times 3 \times (4+5) = 6 \times (4+5)$$
となります。
共通因数が\(2 \times 3\)なので、\(2 \times 3\)をかっこの外に出して、残りをかっこの中で足しあわせます。
じゃあこれはどうか?
$$2 \times 3+2 \times 4+2 \times 5$$
足しあわせる数が三つに増えました。
でも、やっぱり考え方は一緒です。
\(2 \times 3\)の因数は\(2\)と\(3\)。
\(2 \times 4\)の因数は\(2\)と\(4\)。
\(2 \times 5\)の因数は\(2\)と\(5\)ですよね。
だから、共通する因数は\(2\)だけ。
よって以下のような式になります。
$$2 \times 3+2 \times 4+2 \times 5=2 \times (3+4+5)$$
共通因数を持つもの同士を足しあわせるなら、いくつ足しあわせるのであれ、同じ考え方が出来ます。
これが、小学校で習った計算の決まりです。
分配法則の一般化
中学生向けに、かけ算の分配法則を一般化します。
一般化とは、ここまで見てきたようにある特定の数に対する式ではなく、すべての数に対して式で説明できるように、文字で式を表現することだと思ってください。
文字式が出てきますが、難しくはありません。
すでに説明したことを繰り返しているだけです。
かけ算の分配法則を一般化すると、
$$a \times b + a \times c=a \times (b+c)$$
となります。
いままでは、この\(a\)とか\(b\)とか\(c\)に、数字を入れてきました。
中学数学では、文字のまま扱えるようにならないといけません。
でもやってることは一緒なのです。
すでに説明したことから、
$$a \times b \times c + a \times b \times e = a \times (b \times c + d \times e)$$
であることも分かってもらえるでしょうし、
$$a \times b \times c + a \times b \times d = a \times b \times (c+d)$$
$$a \times b+a \times c+a \times d=a \times (b+c+d)$$
というのも、おわかりでしょう。
分母が違う分数の足し算を通分して計算する理由
さて、これでかけ算の分配法則のおさらいが終わりました。
次は、この法則が分数計算とどう関係するのかを説明しなければなりません。
分数の計算をするとき、分母が違う場合は通分をしますよね。
$$\frac{1}{2} + \frac{1}{3} = \frac{3}{6} + \frac{2}{6}$$
というように、分母を揃えます。
これを通分といいます。
分数の足し算や引き算をするためには、このような操作を行う必要があります。
「なんで通分しないといけないの?」
「どうして通分したら計算していいの?」
など、疑問に思ったことはありませんか。
では、
$$\frac{3}{6} + \frac{2}{6}$$
に注目してみてください。
この式は次のように書き換えることが出来ます。
$$3 \times \frac{1}{6} + 2 \times \frac{1}{6}$$
どうでしょうか?何か気がつきませんか?
\(3 \times \frac{1}{6}\)の因数は、\(3\)と\(\frac{1}{6}\)です。
\(2 \times \frac{1}{6}\)の因数は、\(2\)と\(\frac{1}{6}\)ですね。
ということは、\(\frac{1}{6}\)が共通因数ということになります。
ここからが、かけ算の分配法則の出番です。
\(\frac{1}{6}\)が共通因数ということは、こういう書き方が出来るはずです。
$$3 \times \frac{1}{6} + 2 \times \frac{1}{6} = \frac{1}{6} \times (3+2)$$

共通因数が分数であってはいけない、なんてルールはありません。
そして、\(3+2=5\)であることははるか昔に教わりましたよね。
ということは、
$$\frac{1}{6} \times (3+2) = \frac{1}{6} \times 5 = \frac{5}{6}$$
になるのは当然ですよね?
じゃあ、次の式の流れにもついてこれるはずです。
$$\frac{1}{2} + \frac{1}{3} = \frac{3}{6} + \frac{2}{6} = \frac{1}{6} \times (3+2) = \frac{5}{6}$$
どうでしょうか。
どうしてそうなるのか、分からない所があれば、下のコメント欄で質問してください。
このように、かけ算の分配法則を使えば、通分した分数同士を計算することが出来ます。
ですから、「なぜ通分するのか?」という問いに対しては、
「通分することでかけ算の分配法則を利用できるようになるから」
と答えることが出来ます。
通分するまでは、共通する因数がありません。
共通する因数がなければかけ算の分配法則は使えない。
だから、通分するのです。
だからもし、次のような問題があったとしましょう。
$$\frac{1}{2} + \frac{1}{3} + \frac{1}{6}$$
を計算しなさい。
通分というのは、かけ算の分配法則を利用できる形にするために行います。
与えられた分数の分母は書き換えなければならない、というルールではありません。
この問題に対しては、
$$\frac{1}{2} + \frac{1}{3} + \frac{1}{6} = \frac{3}{6} + \frac{2}{6} + \frac{1}{6}$$
というように通分することになります。
最後の項の\(\frac{1}{6}\)は与えられた問題のままだけど、これは変えなくていいのだろうか、なんて悩む必要はありません。
分数の分母がすべての項で一致すればいいのです。
足しあわせる三つの数に\(\frac{1}{6}\)という共通因数が生まれました。
あとは\(\frac{1}{6} \times (3+2+1)\)というように、かけ算の分配法則を利用することで解決します。
かけ算の分配法則が利用できれば、それでいいのです。
スポンサーリンク
通分した後の分母は何でもよい
でも、こんな風に説明すると、こういうのはどうなんだと言いたくなるかもしれません。
$$\frac{1}{2} + \frac{1}{3} = \frac{18}{36} + \frac{12}{36} =\frac{1}{36} \times (18+12) = \frac{30}{36}$$
ほら、\(\frac{1}{36}\)という共通因数作ったぞ?
共通因数さえ作れば通分は成功なんだろ?
じゃあこれでも文句ないよな?
はい。かまいません。
\(\frac{30}{36}\)は\(\frac{5}{6}\)とイコールで結べますから、この計算は間違いではありません。
ただし、学校では不正解とされるかも知れません。
通例、学校教育では約分可能な分数は、約分した状態で書くことが求められます。
そのため、こういう書き方をすると不正解とされることはあり得ます。
でも、数学的には間違ってはいませんし、場合によっては分母を最小公倍数にしない方が都合のいいこともあります。
普通はやらないけど、やってはいけないというわけではないことだけ、覚えておいてください。
まとめ
いかがだったでしょうか。
分数の足し算、出来るような気がしませんか?
分数の足し算というのは、じつはすでに教わったはずのかけ算の分配法則を応用したものだったのです。
では最後に、このページの重要なポイントをまとめておきます。
かけ算の分配法則とは、「共通する因数を持つ数を足しあわせるとき、かっこの中で、共通しない因数同士を足しあわせ、それを共通する因数にかけてもよい」という意味である。
分数の足し算をするとき、通分をすると、かけ算の分配法則を利用することが出来るようになる。
通分とは、かけ算の分配法則を利用するために行うものである。
それでは、またお会いしましょう。



























ディスカッション
コメント一覧
つまり分母の違う分数同士の 足し算 引き算 は分配法則の形にしないと解けないからということですか?
間違ってたらすいません