ベンフォードの法則 – 世の中は”1″がもっとも高い頻度で登場する

”ベンフォードの法則”を紹介します。
これは、世の中に存在する数字は統計的に、この法則に従って登場するという実に面白い法則です。
ところで、みなさんは1~9の数字で世の中に一番登場する数字はどれだと思いますか?
すべて同じくらいでしょうか?それとも、それぞれの数字で使われている頻度は異なり、例えば”7″が一番よく使われている数字であるということがあり得るのでしょうか?
ベンフォードという人は、大量の数字を調べていくなかである不思議な数字の法則に気づきました。そんなことをここでは紹介していきます。
世の中の数字はベンフォードの法則にしたがって登場する
この世の中には数字が溢れています。身近なところでは、
- テストの点数
- 買い物するときの物の値段
- 目的地まで距離
などです。もっと数字に溢れている業界は、
- 会社の経理
- 株や為替
- パソコンの中のファイルのサイズ
などもあります。
例えば、
73,137
というテキトーな大きな数を書いてみましたが、その先頭の数字は”7″です。
このように世の中に登場する数の先頭(一番大きな桁)の数字で、もっとも登場する頻度が高い数字はなんでしょうか?
1でしょうか?それとも5や9でしょうか?

普通に考えると、
「世の中にはいろいろなことを表す数字があり、どの数字が先頭にくるかなんてほとんどランダムであろう。なので、数の先頭に1~9の数字が登場する頻度は同じだろ」
と考えますよね。
しかし、実際はそうでもないのです。私たちは意図的に特定の数字を使っているわけではないのですが、世の中にはよく数の先頭に登場する数字と、あまり登場しない数字が存在するのです。
そしてその登場頻度は、
「世の中にもっともよく登場する数字は1。その次は2であり、その次が3…、最後の数字(一番登場しない数)は9である」
というふうになるのです!
1から9までの登場する頻度は以下のグラフのように描けます。
このグラフから1が登場する頻度は、30%と一番高いです。
次に、2はその半分ちょっとの18%程度、3はもっと減って約13%…というふうに数字が大きくなるにつれて登場する頻度も低くなっていきます。
一番登場頻度が低い9は約4%となっています。
このように先頭の数字が大きくなるにつれて、出現確率は指数関数的に減少していきます。
指数関数的に減少というのは、下のグラフように”はじめは大きく減少するが、後半にいくにつれて減少量が小さくなる”変化のことです。
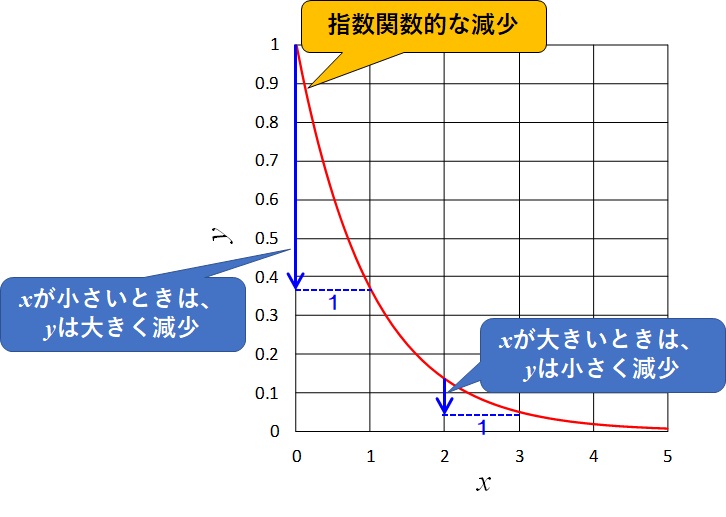
非常に不思議な法則ですね。世の中の数字の先頭はこのような確率で登場しているらしいのです。
確認するには多くの労力を費やしそうな事実ですが、実際の世の中の数字はこの法則にしたがって登場しているのです。
この法則を初めに発見したのはフランク・ベンフォードというアメリカの電気工学者でした。そのため、この法則を”ベンフォードの法則”と呼びます。
スポンサーリンク
数式表現
では、ベンフォードの法則はどのような数式で表せるのでしょうか?
それは、以下の数式で表せます。
$$p_n = \log{\left(1 + \frac{1}{n}\right)}$$
ここで、\(p_n\)は先頭の数字が\(n\)になる確率を表しています。つまり、先頭の数字が\(1\)になる確率は\(p_1\)と表現でき、その値は上の式から、
\begin{align}
p_1 &= \log{\left(1 + \frac{1}{1}\right)}\\
&= \log{\left(1 + 1\right)}\\
&= \log{\left(2\right)}\\
&=0.30103\\
&=30.103 \%
\end{align}
となります。なので、先頭の数字が1になるのは約30%ですね。
残りも計算して、正確な数値を以下の表に示しておきます。
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| \(P_n\) | 0.30103 | 0.17609 | 0.12494 | 0.09691 | 0.7918 | 0.06695 | 0.05799 | 0.05115 | 0.04576 |
ベンフォードの法則を確かめてみる
ベンフォードの法則はにわかには信じられないような法則です。ですので、実際に確認してみました。
調べるには大量のデータが必要ですので、ここではネット上から簡単にダウンロードできる株価と野菜の値段を使って、独自に解析してみます。
株価でチェック
数字といったらまず株でしょう!株価でベンフォードの法則が正しいかを確認してみます。
まずは、無料で株価情報が手に入るサイトから一週間分の株価一覧をダウンロードしてきました。
解析に使った株価の数は3,795個です。これらの先頭の数をカウントしていきます。
結果は下のグラフのようになりました。
驚くほどベンフォードの法則に従っていますね。
7, 8, 9あたりが少し大小関係が逆になっていますが、これはもともと出現確率が低いためと考えられます。
もっと解析に使う株価の数を増やせば、さらに滑らかなグラフが描け、キレイな指数関数が得ることができると思われます。
野菜の値段でチェック
野菜の値段でも確認しときましょう。
あるサイトから野菜の値段の一覧をダウンロードして株価と同じように解析しました。
調べた野菜の値段の総数は…すみません忘れました。…がとても多くのデータ(3,000は超えていたと思います)を調べました。
先頭の数の登場頻度は次のグラフのようになりました。
株価の時に比べて”1″の出現確率が25%と小さいですね。その後の減少量も株価の時に比べて緩やかです。
このような若干の違いはありますが、”1″がもっとも出現確率が高く指数関数的に減少していく傾向は同じです。
こちらもほとんどベンフォードの法則が成り立っていると言っていいようです。
このように、やはり自然に表れた世の中の数はベンフォードの法則に従って登場するといって良いようです。
この「自然に」というところがキーポイントなので、覚えておいてくださいね。
スポンサーリンク
ベンフォードの法則はどんなことに使われているのか
ベンフォードの法則は世の中のどんなことに役立っているのでしょうか?
わたしの第一印象では、「面白い法則だけど、あんまり実用性はなさそうだぁ」という感じでした。みなさんはどうですか?
しかし、実はベンフォードの法則は”ある不正を暴くため”に大活躍しているのです。
その不正とは、”粉飾決済”です!
粉飾決済とは、会社が税金を払いたくないときにわざと売り上げを低く申請して、払う税金を少なくしようとすることです。(間違ってたらすみません)
粉飾決済は、もちろん犯罪です。
会社が売り上げを申請するときは、何を買って何を売ったかや、利益がどのくらいか、などたくさんの数字が書かれた書類を提出する必要があります。

この書類がなんの人為的な操作がされていない場合は、数字はベンフォードの法則に従うはずです。自然にできた数ですからね。
しかし、会社が数字を売り上げを誤魔化すために、数字に何らかの人為的な操作をしていた場合、それは自然に作り出された数ではありません。
ベンフォードの法則は”自然に”作り出された数の集合でなければ成り立たないため、不正をした場合は法則に従わないのです。
つまり、会社が不正をしているかどうかを調べるには、売り上げなどの書類の数字がベンフォードの法則に従っているかどうかを調べればよいのです。
このようにして、会社の粉砕決済を暴くためにベンフォードの法則は使われているのです。
すごく世の中の役に立ってますね。
まとめ
- ”ベンフォードの法則”は、世の中に自然に登場する数の先頭の数字が出現する頻度(出現確率)を表す法則である
- 世の中の数の先頭の数字は、”1″がもっとも出現確率が高く、数字が増えていくにつれて出現確率は指数関数的に減少していく
- 株価や野菜の価格について調べたが、やはりベンフォードの法則に従っていることを確認した
- ベンフォードの法則は粉飾決済を見破るために使用されている



























ディスカッション
コメント一覧
まだ、コメントがありません