【中学2年数学（式の計算）】単項式と多項式とは – その次数と係数もマスターしよう

2018年5月24日2018年6月11日

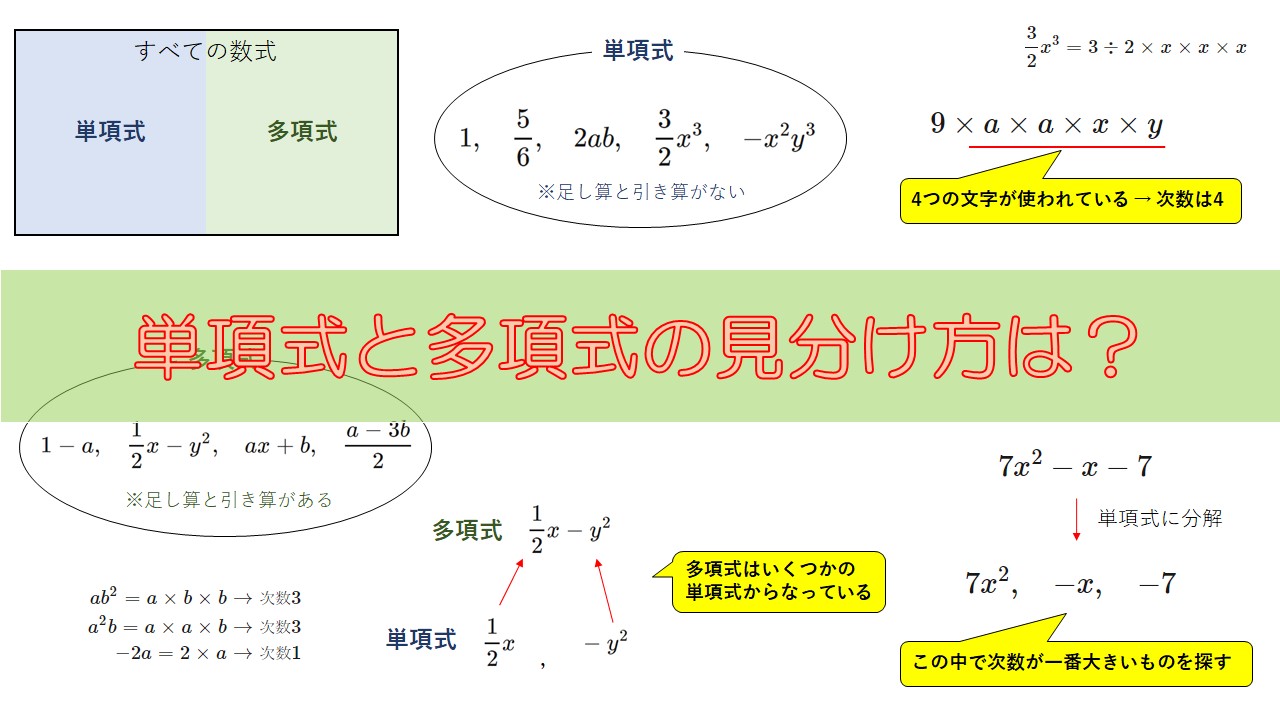
単項式と多項式とは – 違いを見分けれるようになろう

数式には、単項式（たんこうしき）と多項式（たこうしき）の二種類があります。

どんな数式もこのどちらかの種類に必ず属しています。

 

単項式と多項式を、教科書などに書いてあるように言葉で説明すると、

• 単項式 … 数や文字の乗法（掛け算）・除法（割り算）だけで表せる式
• 多項式 … 単項式の和（足し算）・差（引き算）の形として表せる式

となります。

 

言葉での説明より、実際にいろいろな式を見てきながら、理解していきましょう。

 

単項式はこんなの

では、単項式から見ていきましょう。

単項式は、例えば次のようなものです。

\begin{align}
1, \quad \frac{5}{6}, \quad 2ab, \quad \frac{3}{2} x^3, \quad -x^2y^3
\end{align}

この式はすべて単項式ですが、すべての式に共通していることがあります。

 

それは、

足し算や引き算が使われていない

ということです。

 

例えば、\(2ab\)は、

$$2ab = 2 \times a \times b$$

です。

掛け算しか使っていませんね。

 

では、\(\frac{3}{2} x^3\)はどうでしょうか？これは、

$$\frac{3}{2} x^3 = 3 \div 2 \times x \times x \times x$$

であり、掛け算と割り算を使っていますが、足し算と引き算は使われていません。

 

最後に、\(-x^2y^3\)はどうでしょう。

先頭に、\(-\)（マイナス）がついていますが、

$$-1 \times x \times x \times y \times y \times y$$

と表すことができるので、やはり足し算と引き算は使っていません。

 

このように、”足し算と引き算を使っていない式”が単項式であると覚えましょう。

 

多項式はこんなの

次に多項式です。

単項式でないものがすべて多項式ですので、単項式を理解すれば多項式は簡単にわかるでしょう。

多項式は、

足し算や引き算が使われている式

です。

 

下の式は、すべて多項式です。

\begin{align}
1-a, \quad \frac{1}{2}x-y^2, \quad ax+b, \quad \frac{a-3b}{2}
\end{align}

 

足し算や引き算が含まれていることがわかります。

 

上の式リストで、最後の\(\frac{a-3b}{2}\)は、一つの式に見えますが、式を変形すると、

$$\frac{a-3b}{2} = \frac{1}{2}a – \frac{3}{2}b$$

と二つの単項式からなっていますね。

なので、多項式です。

 

このように、”多項式は足し算と引き算が使われている式”ということを覚えましょう。

そして、”多項式はいくつかの単項式からできている”ということも大切です。

 

スポンサーリンク

次数と係数

単項式と多項式を見分けることができるようになったら、次は次数（じすう）と係数（けいすう）をマスターしましょう。

 

次数とは

まずは、次数からです。

次数とは、

掛け合わさっている文字の個数

のことです。

 

例えば、

$$x^2$$

について考えてみましょう。

これは、次のように書き直せます。

$$x \times x$$

\(x\)が2つ掛け合わさっていますね。

なので、\(x^2\)の次数は”\(2\)”ということになります。

$$x^2\text{の次数} = 2$$

 

掛け合わさっている文字は同じである必要はありません。

例えば、

$$ab$$

は、

$$a \times b$$

ですので、これも文字（\(a\)と\(b\)）の2つが掛け合わさっています。

よって、\(ab\)の次数は\(2\)です。

$$ab\text{の次数} = 2$$

 

このような考え方で、次の式の次数を考えてみてください。

$$9a^2xy$$

 

少し難しいですか？

でも大丈夫です。丁寧に一つ一つを分解して、文字の数を数えましょう。

 

これは、掛け算の記号（\(\times\)）を使って表すと、

$$9 \times a \times a \times x \times y$$

ですね。

掛け合わさっている文字は、\(a\)が2つと\(x\)と\(y\)が1つずつの計4つです。

ですので、

$$9a^2xy\text{の次数} = 4$$

となります。

 

一番先頭の”\(9\)”は数字であり、文字ではありません。ですので、これはカウントしないことに注意してください。

 

多項式の次数

ここまでは、単項式の次数について見てきました。

では、多項式の次数はどうでしょうか。

次の式を見てください。

$$7x^2-x-7$$

 

この式は引き算が使われているので、多項式ですね。

この多項式は以下の3つの単項式から作られています。

$$7x^2, \quad -x, \quad -7$$

 

はじめの\(7x^2\)は\(7 \times x \times x\)となるため、次数は\(2\)です。

$$7x^2\text{の次数} = 2$$

次に、二番目の\(-x\)の次数は、

$$-x\text{の次数} = 1$$

ですね。

最後に\(7\)の次数は\(0\)です。数字だけで一つも文字が使われていませんからね。

$$7\text{の次数} = 0$$

 

さて、では元の多項式\(7x^2-x-7\)の次数は何でしょうか？

多項式の次数は、

多項式を作っている単項式の中で、一番大きい次数がその多項式の次数

になります。

 

多項式\(7x^2-x-7\)を作っている単項式

$$7x^2, \quad -x, \quad -7$$

の中で一番大きい次数を持つのは、\(7x^2\)の次数\(2\)でした。

 

よって、多項式\(7x^2-x-7\)の次数は\(2\)となります。

$$7x^2-x-7\text{の次数} = 2$$

 

\(7x^2\)の次数\(2\)と\(-x\)の次数\(1\)を足して、\(2+1=3\)としてはいけませんので、注意してくださいね。

 

練習してみよう

では、練習で次の式の次数を考えてみてください。

$$ab^2 + a^2b – 2a$$

 

まずは、単項式に分解します。すると、

$$ab^2, \quad a^2b, \quad – 2a$$

です。

それぞれの次数を計算すると、

\begin{align}
ab^2 = a \times b \times b \rightarrow \text{次数}3 \\
a^2b = a \times a \times b \rightarrow \text{次数}3 \\
-2a = 2 \times a \rightarrow \text{次数}1
\end{align}

です。

一番大きい次数ははじめの2つの”次数\(3\)”ですね。

よって、\(ab^2 + a^2b – 2a\)の次数は\(3\)となります。

$$ab^2 + a^2b – 2a\text{の次数} = 3$$

 

どうでしたか？できましたか？

 

\(1\)次式や\(2\)次式

• 次数が\(1\)の式を、\(1\)次式（いちじしき）
• 次数が\(2\)の式を、\(2\)次式（にじしき）

と言います。

これは、\(3\)以上も同様です。

 

例えば、上の練習問題の式\(ab^2 + a^2b – 2a\)の次数は\(3\)でしたね。

なので、これは\(3\)次式ということになります。

$$ab^2 + a^2b – 2a \rightarrow 3\text{次式}$$

 

係数（けいすう）とは

次は、係数です。

係数は簡単です。

 

文字についている数字のことを係数（けいすう）

と呼びます。

 

例えば、

$$6xy$$

であれば、文字（\(xy\)）についている数字は\(6\)ですね。

なので、\(6xy\)の係数は\(6\)ということになります。

$$6xy\text{の係数} = 6$$

 

では、次の式の係数はなんでしょうか？

$$- \frac{2}{5} a^2b^3$$

文字以外の部分が係数ですので、この式の係数は、

$$- \frac{2}{5} a^2b^3\text{の係数} = -\frac{2}{5}$$

ですね。

 

では、多項式に対して係数とはどこになるのでしょうか？

実は、多項式に対して、係数というものはありません。

「この多項式の係数はなんでしょう？」という問題は出ないということです。

係数は、単項式のためだけのものなのですね。

 

まとめ

ここまでで学んだあなたは、単項式と多項式を見分ける問題を100%解けるようになっていますよ。

そして、次数や係数も、これから習う計算問題を解くためにとても重要な考え方です。

ぜひ、ここでマスターしてくださいね。

 

では、最後にここで学んだ重要ポイントを復習して終わりましょう。

では、また会いましょうね。