【中学3年数学(多項式)】因数分解するときの共通因数ってナニモノ?

- そもそも因数分解って言葉がわからない
- 因数分解って何すればいいの
- 共通因数もわからない
- もういやだ
中学生でも因数分解は学びますが高校に入ったらさらに高度な因数分解が待っています。
「今、中学生だけど因数分解できないよ」っていう人。「高校生だけど因数分解できないよ」っていう人。
因数分解は練習すれば誰でもできます。頭がいいとか関係ないんです。
繰り返した数が多ければ多いほど理解できる単元です。苦しいですが、反復しましょう!
必ずできるようになります。
因数分解(いんすうぶんかい)ってなに?
中学数学でも高校数学でも、よく「因数分解」という言葉を聞きますが、そもそも因数分解とはなんなのでしょう?
まず前半の因数というのは簡単にいうと掛け算のパーツのことです。
例えば、
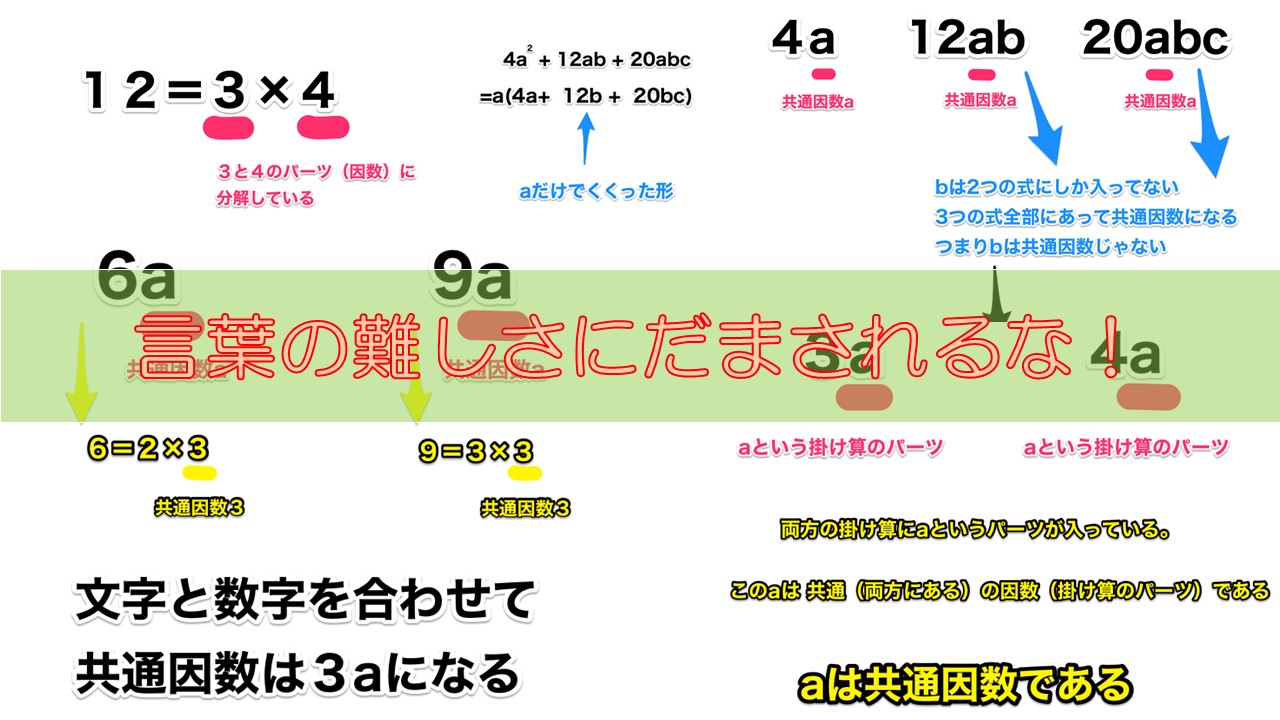
$$12=3 \times 4$$
と表すことができますね。
これは\(12\)を\(3\)と\(4\)というパーツに分解したということです。
このとき、\(3\)と\(4\)の数字それぞれが因数というものになります。

このように\(12\)を\(3\)と\(4\)の掛け算に分解している状態を因数分解と言います。
では、他の例もやってみましょう
$$18=A \times B$$
さて\(A\)と\(B\)には何が入るでしょうか?
「\(2 \times 9\)」や「\(3 \times 6\)」、なかには「\(18 \times 1\)」のなった人もいるのではないでしょうか?
はい、これもどれもが因数分解です。

\(18\)という数字を2つ以上の数字の掛け算だけで表すことができたからです。
つまり、
因数分解というのは、掛け算のパーツに分解すること
です。覚えておきましょう!
スポンサーリンク
共通因数(きょうつういんすう)って何?
文字の共通因数
では、次に共通因数について理解しましょう。
また名前が難しいので、言葉の意味を理解することが大切です。
まず、”因数”というのは先ほど説明した通り、掛け算のパーツです。
”共通”というのは両方(全て)にあるということです。
言い直すと、「両方にある掛け算のパーツ」ということになります。
では、この言葉を頭に入れながら、共通因数を数字で見て行きましょう。
\(3 \times a\)と\(4 \times a\)という二つの式があります(記号は省いて以下\(3a, 4a\)とします)
$$3a, \quad 4a$$
この式では同じ文字が入っているのがわかりますか?
そう共通の\(a\)が入っていますね。
両方の掛け算に\(a\)というパーツが入っています。
この\(a\)のことを共通因数と言います。

数字の共通因数
では、次に数字の共通因数を考えて見ましょう。
\(4\)と\(12\)で考えましょう。
まず、それぞれの数字を掛け算に直してみると、
- \(4 = 2 \times 2\)
- \(12 = 2 \times 6\)
と分解できますね。
この\(2 \times 2\)と\(2 \times 6\)で共通因数はどれになるでしょうか?
そう\(2\)ですね。共通のパーツが共通因数でした。
ここであることに気づいた人もいるでしょうか?
「あれ?\(4 = 4 \times 1\)にもできるし、\(12 = 4 \times 3\)にもできるから共通因数は\(4\)じゃないの?」
と…
はい。これは\(4\)も共通因数なんです。
「共通因数がいっぱいあるなんでめんどくさいなぁ」
と思った人もいるでしょう。
どっちの共通因数を使うかは、問題などに変わってきますが、ここでは、なるべく大きい数字の共通因数を使うと覚えておきましょう。
その方が都合が良いことが多いからです。この理由は後で説明します。
文字と数字の共通因数
では文字と数字を混ぜてみましょう。
\(6a\)と\(9a\)の共通因数を探します。
$$6a, \quad 9a$$
まず、\(a\)はすぐに共通因数だと気づくはずです。
しかし、ここで終わってはいけません。
\(6\)と\(9\)も考えましょう。
\(6\)と\(9\)はぞれぞれ、
- \(6 = 2 \times 3\)
- \(9 = 9 \times 3\)
に直せるので、共通因数は\(3\)になります。
この二つ(\(3 \times a\))を合わせると、
\(6a\)と\(9a\)の共通因数は\(3a\)
ということになります。
文字と数字がある場合は別々に考えて最後に合わせましょう。
3つの式から共通因数を探す
\(a\), \(12ab\), \(20abc\)の共通因数を探そう
文字と数字が入った共通因数の見つけ方はできるようになりましたか?
では最後に3つの式の共通因数を考えてみましょう。
さて、今度は3つの式がある場合です。以下のような3つを考えます。
$$4a, \quad 12ab, \quad 20abc$$
文字も増えましたね。
でも落ち着いてください。やることは一緒です。
まずは文字からいきましょう。
下の図にあるように\(a\)は3つ全てにあるので共通因数です。
\(b\)は\(4a\)の式に入ってないので共通因数ではありません。
なので、文字の共通因数は\(a\)になります。
次に数字を考えましょう。
3つの数字を考えると\(4\)が共通因数になります。
ここで、先ほど出た話を思い出しましょう。
「\(2\)も共通因数なのだから\(2\)ではダメなの?なんで?」
そんな疑問が出てくるでしょう。
あとで説明しますが、とりあえず、\(4\)の方が大きいから\(4\)としておきましょう。
あとで「なるほど!」と納得できます。
さて、文字と数字のそれぞれ共通因数を見つけることができました。
合わせて答えは\(4a\)になりますね。
ここまではどうでしょうか?
共通因数と言葉で聞くと難しい感じがしますが、要するに「同じ数、文字を見つけようね」ということです。
スポンサーリンク
共通因数を使っていろいろな因数分解にチャレンジ
では、次に共通因数を見つけて因数分解をしてみましょう!
\(2a+5ab\)の因数分解
さて、因数分解と共通因数は理解できたでしょうか?
今度は、
$$2a+5ab$$
の因数分解をしてみましょう。
まず復習ですが、因数分解とは掛け算のパーツに分解することでしたね。
この式を見てみると掛け算ではない部分がありますね。
そう。\(+\)が入っています。
こいつは因数分解を邪魔する天敵です。
では、この式を掛け算のパーツに分解するにはどうしたら良いか。
それは共通因数をくくることです。
ちょっとややこしくなってきましたね。
でも落ち着いて。やることはさっきと何も変わりません。
まず共通因数を見つけましょう。
\(2a\)の\(5ab\)共通因数は\(a\)ですね。
では\(a\)を式からくくって見ましょう!
さて、これで因数分解は完了しました。
「え?これだけ?\(+\)が残っているじゃない?」
そう思う人は多いでしょう。
しかし数学の中では( )をつけるとそれは1つの因数(パーツ)として扱うことができます。
つまり、この式は掛け算だけに分解したということが言えるのです。
文字の2乗を含む共通因数
共通因数の因数分解に慣れてきましたか?
では、こんな式だったらどうでしょうか?
$$2a^2 +5ab$$
この場合は以下のように考えましょう。
まず、
$$a^2=a \times a$$
となります。
よって元も式を書き直すと、
$$2a^2 +5ab = 2aa +5ab$$
となります。
この式で\(a\)は左に2つ、右に1つ入っていますよね。
こうゆうときは、式から\(a\)を一個ずつ取り出せます。
$$a (2a+5b)$$
右の式には\(a\)が1個しかありませんから、左からも1個しか取り出せないのです。
これで終わりです。
\(a(2a+5b)\)=\(2a^2+5ab\)
実際にできた答えを展開すると元の式に戻るので、答えが正しいと確認できます。
間違いやすい問題
今から間違いやすい問題を1つ出します。
特に難しい問題ではないので、頭の片隅に残しておきましょう。
\(6a+3\)を因数分解しなさい。
共通因数を探します。共通因数は\(3\)なので答えは
\(3(2a)\)
これは正しいですか?何か忘れていますね。
そうです。+1を忘れているんです。
正しくは\(6a+3\)=\(3(2a+1)\)です。 ※+1を忘れないように
スポンサーリンク
\(4a^2+12ab+20abc\)を因数分解しよう
この問題で共通因数の因数分解の話は終わりです!頑張りましょう。
やり方は何も特別なことはありません。今まで通りの考え方で十分解けます。
まず\(a\)が全ての式に入っているので\(a\)をくくり出しましょう。
大丈夫ですよね?
では次に数字を考えていきましょう。
すべて\(4\)でくくると下の図のようになります。
これで因数分解完成です!
\(4\)ではなく\(2\)でくくってみる
さきほど最後に\(4\)でくくりましたが、\(2\)も共通因数です。
なので\(2\)でくくってもいいのではないでしょうか?
共通因数\(2\)でくくった場合もやってみましょう。
\(2\)でくくると以下のようになります。
さて何か違和感を感じないでしょうか?
そう、( )の中の式はまた\(2\)でくくることができるんですね。
\(2\)を( )の外に出すと、前と同じ結果が得られます。
つまり最初に言っていた共通因数は大きな数を選ぶというのは、結局計算結果一緒になるなら、最初からおおきん数を選んで、計算の数を減らそうね!ということだったのです。
まとめ
因数分解の意味、やり方、共通因数の意味を説明してきました。
式が複雑のなってもやることの1つ1つはシンプルであることがわかりました。
では、以下に重要なポイントをまとめて終わりましょう。
共通因数とは難しい言葉ですが、簡単にいえば式にある同じ数、文字のことです。
それを難しく言ってるだけです。
因数分解も同じです。
掛け算だけに分解しようねって言ってるだけなんです。
- 共通因数 ⇒ 式にある同じ数、文字のこと
- 因数分解 ⇒ 掛け算に分解すること
数学は難しい言葉を使ってきますが、中身は簡単な言葉で説明できることが多いです。
言葉の難しさに負けず、意味を理解しましょう!

























ディスカッション
コメント一覧
16×14=(15+1)×(15-1)=15×15-1=1×1
=(20-5)×(20-5)-1
=400-2×20×5+5×5=400-200+25-1=224
19×19=(20-1)×(20-1)=20×20-2×20×1+1×1
=400-40+1=361
とすると暗算でできますね。
13×13×13=(10+3)^3=10×10×10+3×10×10×3+
3×10×3×3+3×3×3=1000+900+270+27=2197
とすれば三乗の計算も楽ですね
まだ習ってなくても凄く分かりやすい。