【中学数学】計算間違いを劇的に減らす具体的な方法

2019年9月2日

自分の計算レベルを超えて途中式を省略しない

計算ミスを減らすために、まず実践して欲しいのは、

自分の計算レベルを超えて、途中式を省略しない

ということです。

 

一次方程式の例

次の問題を解きながら具体的に説明していきます。

\(3x – 4 = 7x + 12\)

のような計算問題があったとします。中学1年生の初期で習う一次方程式ですね。

 

まずは、この問題を途中式を省略せずに丁寧に解いていきましょう。すると、以下の3ステップで解くことになります。

【ステップ１】\(x\)が付いている項を左辺に、数字だけの項を右辺に持ってきて、

\(3x – 7x = 12 + 4\)

とします。

【ステップ２】左辺と右辺をそれぞれ計算して、

\(-4x = 16\)

とします。

【ステップ３】両辺を\(-4\)で割って、

\begin{align}
-4x \div (-4) & = 16 \div (-4) \\
x & = -4
\end{align}

として、答えが求まりました。

丁寧に省略せずに書くとこうなります。つまり、計算の途中式は以下のようになります。

\begin{align}
3x – 4 &= 7x + 12 \\
3x – 7x &= 12 + 4 \\
-4x &= 16 \\
-4x \div (-4) &= 16 \div (-4) \\
x &= -4
\end{align}

ここまで丁寧に途中式を書いていけば、そうそう計算間違いはしないでしょう。

 

しかし、実際のテストで計算する場合はどうでしょうか。

上のステップで書いた式をテストのときもいちいち書いていますか？

もしかして、ステップ１は暗算して、いきなりステップ２の式から始めようとしていませんか？

 

【ステップ１を飛ばした途中式】
\begin{align}
3x – 4 &= 7x + 12 \\
-4x &= 16 \\
x &= -4
\end{align}

 

もしかするとこれがあなたの計算ミスに繋がっているかもしれません。

特に、この計算例のようにステップ１を飛ばすと、移項時の符号の変え忘れが起きやすいです。

 

途中式を飛ばすことが悪いとは言いません。

これでも間違えずにできるくらい計算に慣れている人であれば、時間短縮としてどんどん途中式は省略していいです。

しかし、少しでも間違える可能性がある計算ステップは暗算せず、確実に途中式は書くように気を付けてみてください。

途中式は面倒でも書く！

です。

 

一つの途中式を書くときは、一つだけの操作

”途中式は面倒でも書く”を実践するとき、どこまで詳しく書けばいいの？と思うかもしれません。

そこで、自分は計算ミスが多いほうだな～と思っている人は、

一つの途中式を書くときは、一つだけの操作をする

を意識してみてください。

 

どういうことかを具体的に説明しましょう。以下の問題を考えます。

$$5(x + y) – 2(x – 3y)$$

解き方のステップとしては、以下の順番になることが分かります。

1. 分配法則を使って括弧を外す
2. 同じ文字を持つ項同士を並べる
3. 同じ文字を持つ項同士を足す、もしくは引く

「一つの途中式を書くときは、一つだけの操作をする」とは、このステップ１～３ごとに途中式をちゃんと書くということです。

 

まず、ステップ１（括弧を外す）は、

\begin{align}
5(x + y) – 2(x – 3y) = 5x + 5y – 2x + 6y
\end{align}

です。

次に、ステップ２（同じ文字を持つ項同士を並べる）を行うと、上の式の右辺が、

\begin{align}
5x + 5y – 2x + 6y = 5x – 2x + 5y + 6y
\end{align}

となります。

最後に、ステップ３（同じ文字を持つ項同士を足す、もしくは引く）は、上の式の右辺が、

\begin{align}
5x – 2x + 5y + 6y = 3x + 11y
\end{align}

となり、これで答えがでました。

 

つまり、自分のノート（テストであればテスト用紙）には途中式は以下のように書かれているはずです。

\begin{align}
5(x + y) – 2(x – 3y) &= 5x + 5y – 2x + 6y \\
&= 5x – 2x + 5y + 6y \\
&= 3x + 11y
\end{align}

このように、次の途中式に移るときは、一つの操作だけをすることを心掛けてください。

 

これを、ステップ１（括弧を外す）とステップ２（同じ文字を持つ項同士を並べる）を一気にやって、計算式をいきなり、

\begin{align}
5(x + y) – 2(x – 3y) = 5x – 2x + 5y + 6y
\end{align}

から始めると計算ミスが多くなってしまいます。

一つの途中式は、一つの操作（１ステップ）だけ

 

「解き方は分かっていたのに、また間違えたな～」と思うことが多い人は、まずはこれから実践してみてくださいね。

 

スポンサーリンク

=は縦につなぐ

次は、途中式の書き方について、ちょっとしたクセをつけましょう。それは、

\(=\)で式を繋ぐとき、縦に式を繋いでいく

ということです。

 

例えば、以下の式を解いてみましょう。上で一度出てきた式と同じです。

$$5(x + y) – 2(x – 3y)$$

解き方は、

1. 括弧を外す（分配法則）
2. 同じ文字を持つ項同士を並べる
3. 同じ文字を持つ項同士を足す、もしくは引く

でした。

これを、以下のように途中式を横に並べて書くことはできるだけ避けましょう。

$$5(x + y) – 2(x – 3y) = 5x + 5y – 2x + 6y = 5x – 2x + 5y + 6y = 3x + 11y$$

 

そうではなく、以下のように縦に式を繋いでいきます。

\begin{align}
5(x + y) – 2(x – 3y) &= 5x + 5y – 2x + 6y \\
&= 5x – 2x + 5y + 6y \\
&= 3x + 11y
\end{align}

明らかにこっちの方が見やすいことが分かると思います。

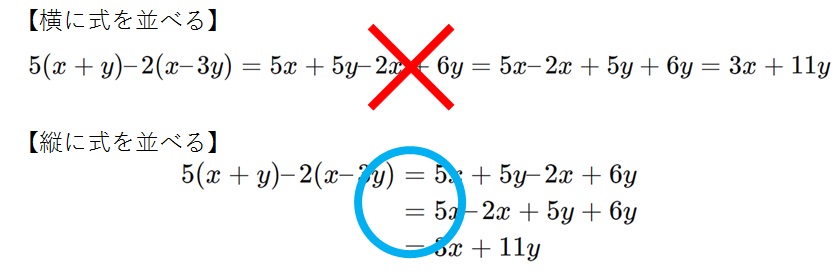
これを気をつけるだけで、計算ミスは減ります。

さらに、解いた後も式が見やすい形で残っているということは、見直しもしやすいということです。

 

実際に試験のときなどは、紙面のスペースの関係上、しかたなく横に式を繋げるしかないときもありますが、できるだけ縦に式を繋げることを意識してやってみてくださいね。

 

一度計算ミスしたものは、なぜミスをしたのかを復習する

計算ミスは誰しも経験があることです。

しかし、計算間違いをした問題に対して、大半の人が

「これは本当は分かっていたから、見直さなくていいや！」

と思い、復習をしません。

 

しかし、単なる計算ミスでもなぜ計算ミスをしたかをきちんと把握することが重要です。

その理由は、人は同じような計算ミスを実は繰り返していることが多いからです。

 

計算ミスの原因は人それぞれです。例えば、

• 自分で書いた文字を読み間違って進めていた（例えば\(6\)を\(0\)と読んでいた）
• \(3 \times 8\)をなぜかいつも\(=27\)と思ってしまう
• \(-2(x-y)=-2x-2y\)としがちである（符号が違う）

などです。このようにその人特有のクセを持っています。

 

「どんな問題や計算が出てきたときにミスが多いのか」という自分の計算ミスの原因（クセ）を探してみましょう。

自分のミスのクセを頭の片隅に入れておくだけで、計算時に注意するようになり、計算途中で間違いに気づきやすくなります。

 

スポンサーリンク

 分数の計算は、細かいまま残しておく

次は、分数の計算をするときのコツです。

分数の計算ミスを防ぐには、

「数字は細かいまま残しておく」

です。

どういうことかを実際に計算を解きながら見ていきましょう。

 

例題①

以下の計算を例にしましょう。

$$\frac{3}{10} \times \frac{5}{6}$$

 

あまり良くない計算の例

まずは、あまり良くない例からやっていきます。あなたはこの方法で計算してしまっていませんか？

まず、分母と分子同士を掛け算して、

\begin{align}
\frac{3}{10} \times \frac{5}{6} &= \frac{3 \times 5}{ 10 \times 6}\\
&= \frac{15}{60}
\end{align}

となります。

最後に分数が約分できるかどうかを考えます。

この場合はまず\(5\)で約分できそうです。なので、分母と分子を\(5\)で割って、

\begin{align}
\frac{15}{60} &= \frac{15 \div 5}{60 \div 5}\\
&= \frac{3}{12}
\end{align}

とします。よく見るとまだ\(3\)で割れますので、

\begin{align}
\frac{3}{12} &= \frac{3 \div 3}{12 \div 3}\\
&= \frac{1}{4}
\end{align}

とし、これが答えです。

しかし、この方法はあまり良くありません。何が良くないのか分かりますか？

次に紹介する良い例と比較してみてください。

 

ミスをしにくい計算の方法

もっと計算量を減らし、ミスが起きにくい方法を紹介しましょう。

まず、分母と分子同士を掛け算して、

\begin{align}
\frac{3}{10} \times \frac{5}{6} &= \frac{3 \times 5}{ 10 \times 6}
\end{align}

とするのですが、ここで完全に計算せず、上のような状態で止めておきます。

つまり、\(3 \times 5 = 15\)や\(10 \times 6 = 60\)という計算をまだ行わないのです。

「数字は細かいまま残しておく」

ということですね。

 

もう一度、式の状態を見ると、

$$\frac{3 \times 5}{ 10 \times 6}$$

です。

そして、この時点で分母と分子に約分できる数字はないかをチェックします。

ここで、分子の\(5\)と分母の\(10\)は\(5\)で約分できそうですし、分子の\(3\)と分母の\(6\)は\(3\)で約分できそうです。

 

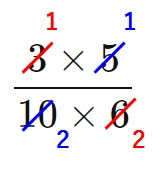
よって、この時点で約分をしてしまって、

\begin{align}
\frac{3 \times 5}{ 10 \times 6} &= \frac{1 \times 1}{ 2 \times 2}\\
&= \frac{1}{4}
\end{align}

とすれば、簡単に答えが出てしまいますね。

 

例題②

次は、分数の足し算も「数字は細かく残す」と意識してやってみましょう。

以下の問題を例題とします。

$$\frac{2}{3} + \frac{1}{12}$$

 

まず、分数の足し算はお互いの項の分母の数を同じにしなければいけませんでした。

この場合は、\(\frac{2}{3}\)の分母を\(12\)にすれば良さそうです。

なので、\(\frac{2}{3}\)の分母分子に\(4\)を掛けて、

$$\frac{2}{3} + \frac{1}{12} = \frac{2 \times 4}{3 \times 4} + \frac{1}{12}$$

とします。

 

ここで、\(3 \times 4\)を計算して\(12\)にしてしまわないことがポイントです。

\(12 = 3 \times 4\)であるのは分かっているため、逆に上式の第2項\(\frac{1}{12}\)の\(12\)を\(3 \times 4\)と分解して計算してしましょう。

すると、

\begin{align}
\frac{2 \times 4}{3 \times 4} + \frac{1}{12} &= \frac{2 \times 4}{3 \times 4} + \frac{1}{3 \times 4}\\
&= \frac{2 \times 4 + 1}{3 \times 4}\\
&= \frac{9}{3 \times 4}
\end{align}

となりますね。分母はまだ\(3 \times 4\)のままです。

 

分子の\(9\)は\(3 \times 3\)ですので、

$$\frac{9}{3 \times 4} = \frac{3 \times 3}{3 \times 4}$$

です。

上の式の右辺を見ると、\(3\)が共通して出てきていますね。これは、一目で約分できると分かります。

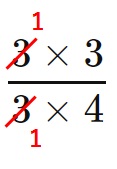
よって、答えは、

$$\frac{3 \times 3}{3 \times 4} = \frac{3}{4}$$

となります。

 

この解き方では、最後まで「\(3 \times 4\)」という形が残っていました。

すなわち、「数字は細かい状態で残す」をやっていたことになります。

 

このように、分数の計算は、

迂闊（うかつ）に計算してしまって、数字を大きくしない！むしろ、細かいままできるだけ残しておく！

ということが計算のコツです。是非実践してみてください。

 

別の計算方法を使って検算する

最後に紹介するのは、

「一度解いた計算方法とは別の方法で検算する」

です。

 

数学のテストで本気で点数を良くしようと思ったら、時間が余ると間違いがないかをもう一度チェックすると思います。

その際、必然的に同じ問題を二度解くことになるのですが、

「同じ計算方法で解かない」

ことをできだけ心掛けてください。

 

その理由は、以下の二つです。

• 同じ計算方法で解くと、同じミスをする可能性があるため間違いに気づきにくい
• そもそも、すべての問題を同じ方法で解く時間なんて余ってない

問題の性質上、どうしても同じやり方で検算しないといけない場合もあるかとは思いますが、できるだけ一度目に解いた方法とは違ったやり方で確認しましょう。

 

計算問題の検算例

例えば、次のような計算問題を検算するとします。

$$3x + 2 = x – 10$$

検算を行う場合、問題は一度解いているはずですので、自分のプリントには、以下のような計算式が書いてあるでしょう。

\begin{align}
3x + 2 &= x – 10\\
3x – x &= – 10 – 2\\
2x &= – 12\\
x &= – 6\\
\end{align}

この解答によれば、答えは\(-6\)となっています。これは合っているのでしょうか？

 

これを検算するときは、上の式と違う方法で検算しましょう。

どんな方法か？

例えば、文字を含んだ方程式を解く問題は、自分の出した答えを問題の式に代入することで正解かを確認できます。

この場合、答えは\(x=-6\)と出しているので、これを問題の式「\(3x + 2 = x – 10\)」の\(x\)に代入します。

すると、

\begin{align}
3x + 2 &= x – 10\\
3\times (-6) + 2 &= (-6) – 10\\
-18 + 2 &= -16\\
-16 &= -16\\
\end{align}

最後は両辺がきちんと同じ数になりましたね。等式がちゃんと成り立っているということです。これで、自分の出した答えは合っているということが分かりました。

 

実際にこの方法をやってみると分かりますが、通常の計算から答えを出すよりもずっと簡単で、計算も速いです。

このように、検算にはよりシンプルな方法を使うことが重要です。

その理由は、もちろん「検算で計算ミスをしたら、元も子もない」からというのが一つ目の理由。

もう一つの理由は、テスト時間内にできるだけ多くの問題をチェックできるようにするためです。

 

大雑把な検算も大事

検算には「この方法で検算するのが正解！」みたいなものはありません。

しかし目的によって検算方法を変えることは重要です。

例えば、「答えは何か」よりも、とにかく「合っているのか？間違っているのか？」だけを知りたい場合があります。

時間が無いときは、間違えているかもしれない箇所をすばやく探し出して修正することが、少しでも点数を上げる有効な方法だからです。

 

そんなとき、大雑把な感覚も大事にしましょう。

例えば、以下のような文章問題があったとします。

この問題に対する自分の解答を見ると、\(x=850\)となっています。

どうでしょうか？この答えは合っていると思いますか？間違っていると思いますか？

1秒で答えてみましょう。

 

そうです。間違いです。

\(x=850\)ということは、サトシ君は鉛筆を850本買ったことになります。

ここで、すぐに次のようなことを思えたらオッケーです。

• 鉛筆を850本も買うとか日常じゃありえないな。
• 普通は1000円で850本も鉛筆を買えないんじゃないか。
• これじゃ、鉛筆1本が1円ちょいじゃん！安っ！

ということで、「この解答は間違ってる可能性が高いな。もう一度計算しなおそう」となるわけです。

 

少し難しい言葉で表現すると、自分の出した答えが”もっともらしいか”を直観で判断することも重要です。

 

では、最後に次の確率の問題を読み、解答が合っているかを1秒で判断してみてください。合っているか、間違っているだけでいいですよ。

どうでしょうか？1秒で答えましょう。

 

この解答は、間違いですね。

\(\frac{3}{10}\)ということは、10回の試したら3回は3連続で同じ目が出るということです。

そんな高確率で同じ目が連続3回も出ませんよね。経験的に明らかに間違っていることが分かるわけです。

 

ちなみに、正解は\(\frac{1}{36}\)です。約2.7%の確率ですね。100回試したら2回か3回はなるという結果です。

私の直感では、だいたいそんなもんのような気もしますし、思ったよりも少し高いかなぁ～という気もします。

 

スポンサーリンク

まとめ

「計算間違いを減らしたいなぁ～」と感じている人は、以下のことに気を付けてみてください。

• 自分の計算レベルを超えて途中式を省略しない
• =は縦につなぐ
• 一度計算ミスしたものは、なぜミスをしたのかを復習する
• 分数の計算は、細かいまま残しておく
• 別の計算方法を使って検算する

 

どれも有効な方法ですが、まずは自分の気に入った方法から試してみると良いですよ。

どれから実践するか迷っている人は、「自分の計算レベルを超えて途中式を省略しない」から初めてみてください。