【中学2年数学(確率)】「じゃんけん」の確率を求める問題をわかりやすく解説

- 確率の問題で、「じゃんけん」が登場した問題の解き方のコツが知りたい人
- 確率の問題の解き方の基礎を学びたい人
中学2年生の数学で習う「確率」の中で「じゃんけん」が登場する問題について詳しく説明していきます。
「じゃんけん」の確率を求める問題は、簡単そうに思えて、実は少し難しかったりします。
ここでは、「2人でじゃんけんする場合」と「3人でじゃんけんする場合」の基本的な問題の解き方をマスターして、テストで点が取れるように実力をつけていきます。
2人でじゃんけんした場合の確率の問題
じゃんけんは、2人以上であれば何人でもできますが、まずはもっとも単純な2人でじゃんけんをした場合の問題から考えていきましょう。

次の例題を解いてみましょう。
AさんとBさんが2人で一回だけじゃんけんをするとき、以下の確率を求めよ。
- あいこになる確率は?
- Aさんが勝つ確率は?

私は、じゃんけんの問題に限らず、中学の確率の問題は「樹形図」を使って解くことをオススメしています。樹形図とは、下の図のようなものでしたね。覚えていますか?
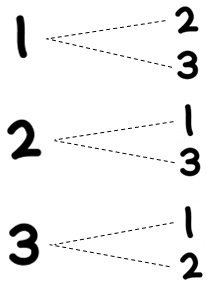
樹形図を忘れた人は、まずは以下の記事から学んでみてください↓
どんな問題もこの樹形図を描くことからはじめましょう。
では、例題①について、樹形図を描いてみましょう。
Aさんが出す手は「グー」「チョキ」「パー」の3つであり、それに対して、Bさんも「グー」「チョキ」「パー」の3つを出す可能性があるので、以下の図のようになります。
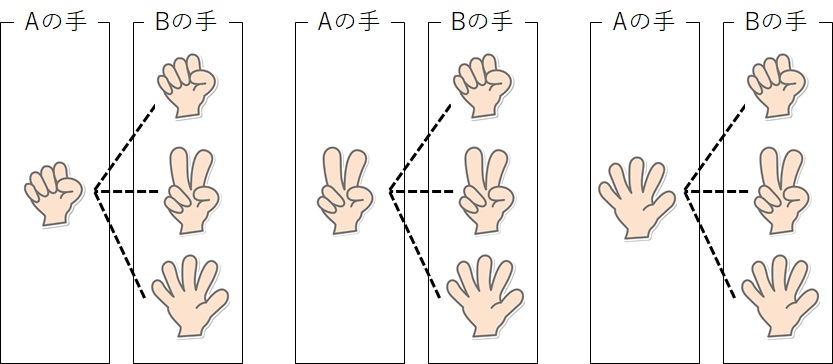
ただし、実際のテストなどで樹形図を描くときは、上の図のようにいちいち手のイラストを描いている時間はありません。テストなどの実践では下の図のように文字や記号で書くようにすればいいでしょう。※樹形図は自分がわかればどのように書いてもかまいません。
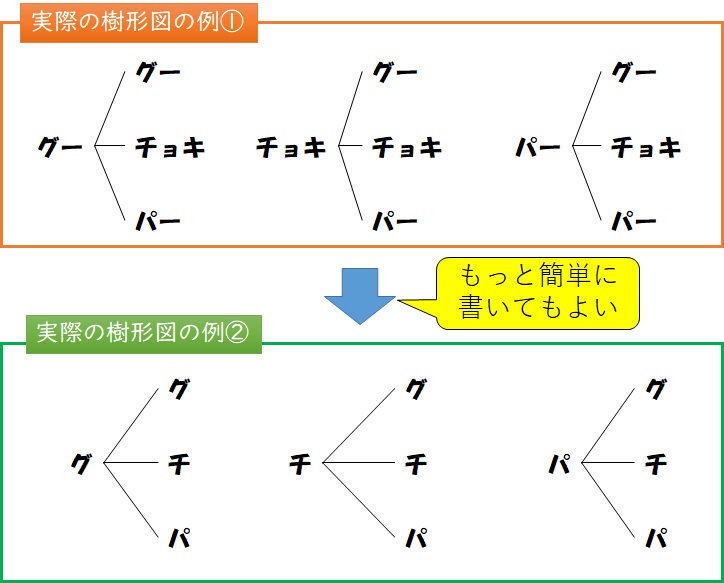
これから、すべての組み合わせは9通りであることがわかります。
問題の1問目「あいこになる確率は?」
問題の1問目「あいこになる確率は?」を調べるため、あいこの場所に印をつけると、
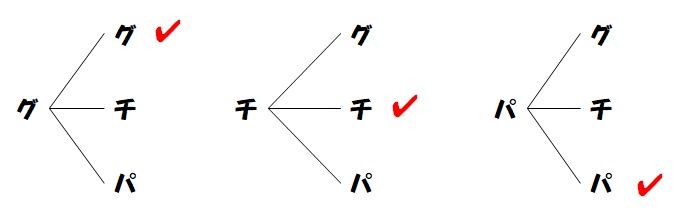
ですね。組み合わせの数は3つです。
すべての組み合わせが9通りで、その中のあいこになる確率が3通りですので、
$$\text{あいこになる確率} = \frac{3}{9} = \frac{1}{3}$$
となります。これが一つ目の問題の答えです。
問題の2問目「Aさんが勝つ確率は?」
2問目は、Aさんが勝つ確率です。この場合も考え方は「あいこ」のときとまったく同じで、樹形図にAさんが勝つ場合をチェックしていきます。
すると、
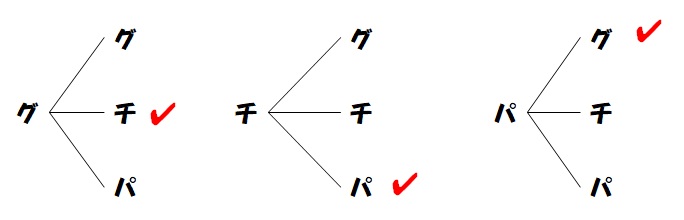
となり、Aさんが勝つ組み合わせは3通りですね。
すべての組み合わせが9通りで、その中のAさんが勝つ確率が3通りですので、
$$\text{その中のAさんが勝つ確率} = \frac{3}{9} = \frac{1}{3}$$
となります。これが2つ目の問題の答えです。
ここまでは、比較的簡単に感じたのではないでしょうか?
基本は、間違えずに樹形図を描くことです。それさえできれば、あとは問題に合わせて組み合わせの数を数えていけば、必ず正しい答えにたどり着けます。
次章からは、じゃんけんする人数を3人に増やします。じゃんけんする人数が増えると難易度も上がっていきますが、基本は変わりません。
「樹形図をしっかり描いて、組み合わせの数を数える!」
これが基本です!
スポンサーリンク
3人でじゃんけんした場合の確率の問題
じゃんけんをする人数が3人の場合を考えていきましょう。テストなどに出題されるじゃんけんの問題では、「3人」が登場する場合がもっとも多いと思います。
ですので、ここで紹介する問題は非常に重要です。一つ一つ確実に理解しながら進みましょう。
では、例題です。
Aさん、Bさん、Cさんの3人で1回じゃんけんをしました。このとき、以下の確率を求めなさい。
問題1:あいこになる確率を求めよ
問題2:Aさんだけが勝つ確率を求めよ
問題3:Bさんが勝つ確率を求めよ
問題4:誰か2人が勝つ確率を求めよ
おまけ問題:BさんとCさんの2人が同時に負ける確率を求めよ
全部で「4つの問題+おまけ」があります。3人でじゃんけんするといろんな手のパターン(組み合わせ)が出てきますので、出題される問題の種類も増えるんですね。
でも、解き方は同じです。丁寧に樹形図を使って解いていきます。
まずは、すべての組み合わせを樹形図に描いていきましょう。
A,B,Cさんの出す手の組み合わせを考えていくと、「結構な数の組み合わせになるなぁ」ということがわかります。
そのようなとき、ミスをせずに樹形図を描いていくコツは、自分の中でルールを作って描いていくことです。
樹形図の書き方は、以下の記事で詳しく説明しているので参考にしてください。
まずはAさんが「グー」を出したとき、どのようになるかを考えます。
そのとき、Bさんは「グー」「チョキ」「パー」が出せますので、以下の図のようになるでしょう。
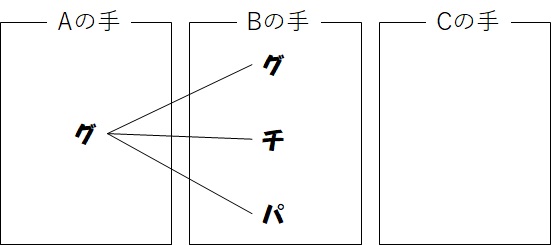
さらに、Bさんが出したそれぞれの手に対して、Cさんが「グー」「チョキ」「パー」のどれかの手を出すので、
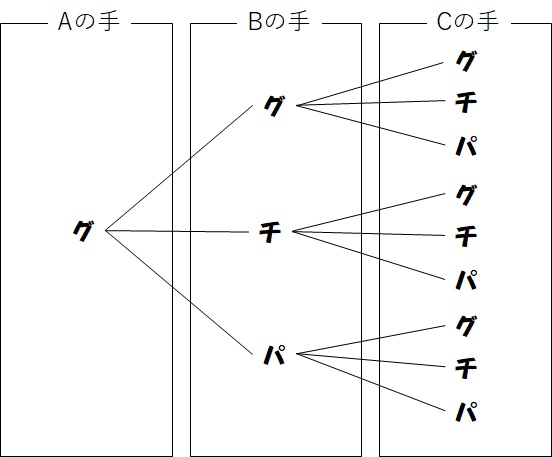
となります。
同じように、今度はAさんが「チョキ」を出したときを樹形図にすると、
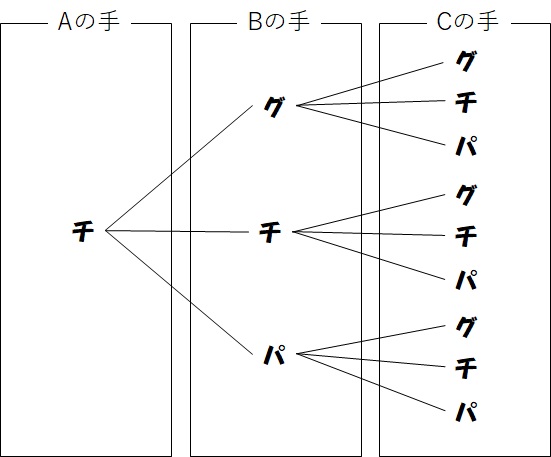
となります。
さらに、Aさんが「パー」を出したときを樹形図にすると、
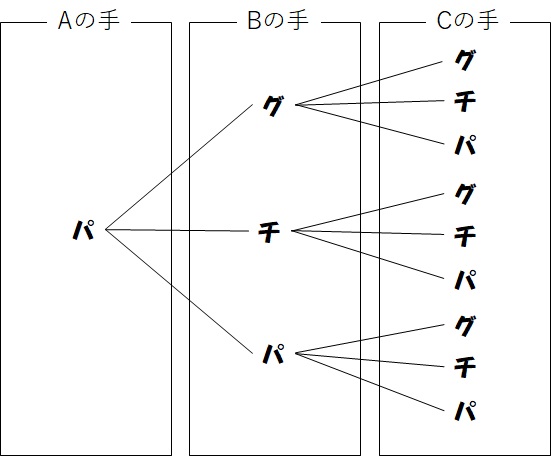
となります。
これで、すべての組み合わせが書き出せましたので、まとめると下の樹形図が出来上がります。
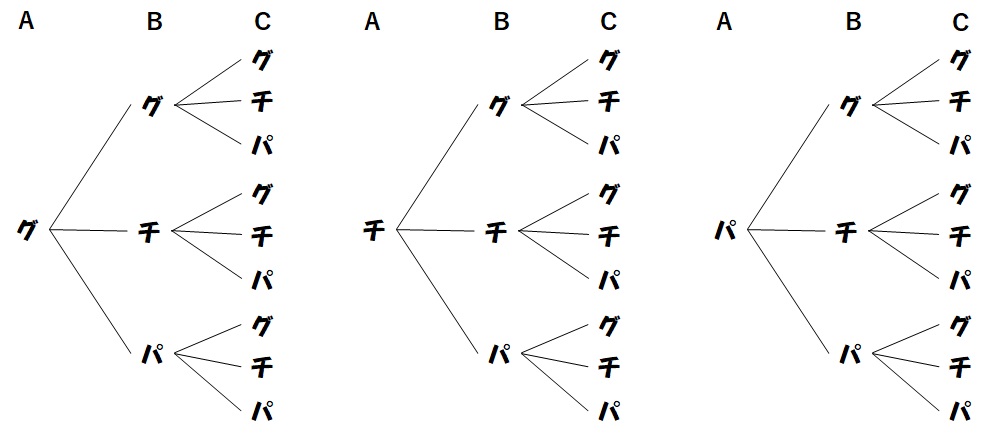
あえて、「Aの手」や四角い枠は省略しました。テストで樹形図を描くときは、そのようなものは描く余裕がないかもしれませんので、大抵はこのように最低限必要なものだけを描くことになるでしょう。
※樹形図に「このように書きなさい!」というものはありません。大事なことは、自分がその樹形図を理解でき、ミスなく問題を解けるかです。
この樹形図から全部の組み合わせの数を数えてみると、27パターンであることがわかりますね。
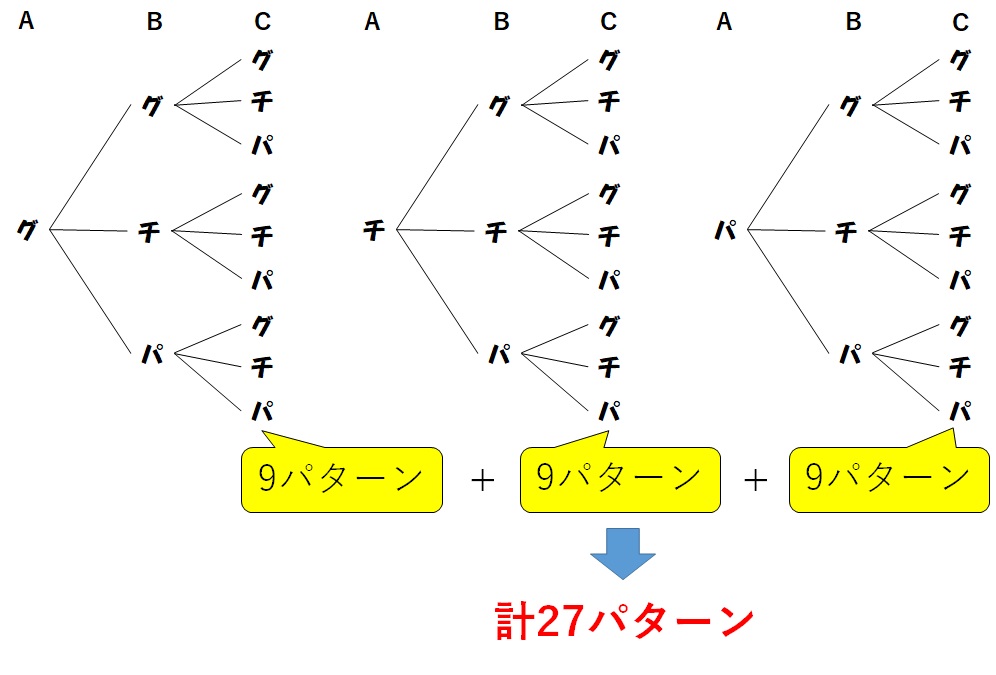
みなさんが普段3人でじゃんけんをするときは、この27パターンのうちのどれかになっているということです。
ここまでわかれば、あとは問題をみて、その問題が求めているパターンを数えていけばオッケーです。
1つずつ解いていきましょう。
問題1:あいこになる確率を求めよ
三人であいこになる場合はどのような場合でしょうか?
まずは、三人とも違う手を出した場合ですね。それと、三人とも同じ手を出した場合です。
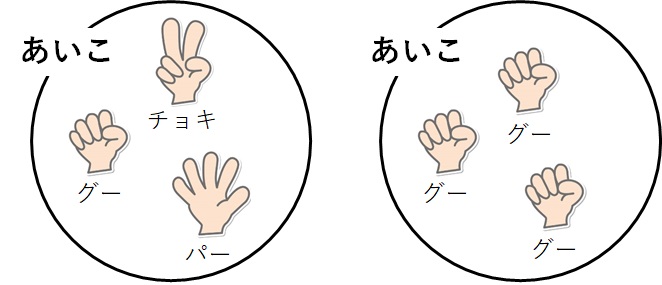
これらのパターンを上で作った樹形図でチェックしていきましょう。すると、
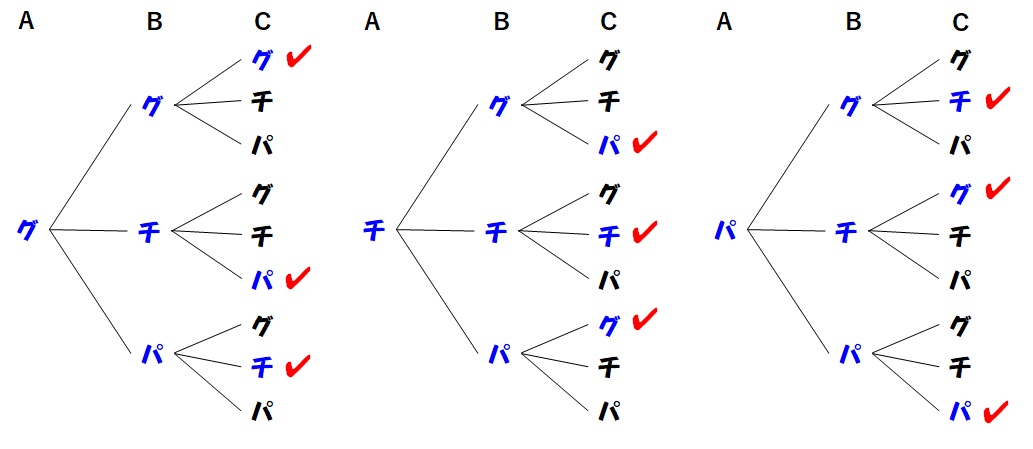
のようになります。
チェックの数を数えると、あいこになる組み合わせの数は9つということがわかりました。
全組み合わせ27つのうち、あいこになる組み合わせは9つですので、確率は、
$$\text{あいこになる確率} = \frac{9}{27} = \frac{1}{3}$$
となります。問題1の答えは\(\frac{1}{3}\)です。
三人でじゃんけんを1回するときは、約30%の確率であいこになるのですね。
自分の経験と照らし合わせてみて、どうでしょうか?
問題2:Aさんだけが勝つ確率を求めよ
続いて、Aさんだけが勝つ確率はどうでしょうか?
この場合は、Aさんが「グー」を出したとき、残りの二人は「チョキ」を出していなければいけません。
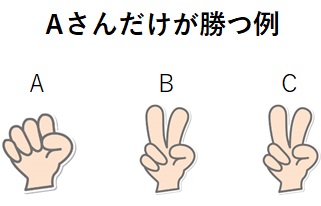
同じように、
- Aさんが「チョキ」を出したとき、残りの二人は「パー」
- Aさんが「パー」を出したとき、残りの二人は「グー」
を出す場合にAさんだけが勝ちます。これを樹形図にチェックしましょう。
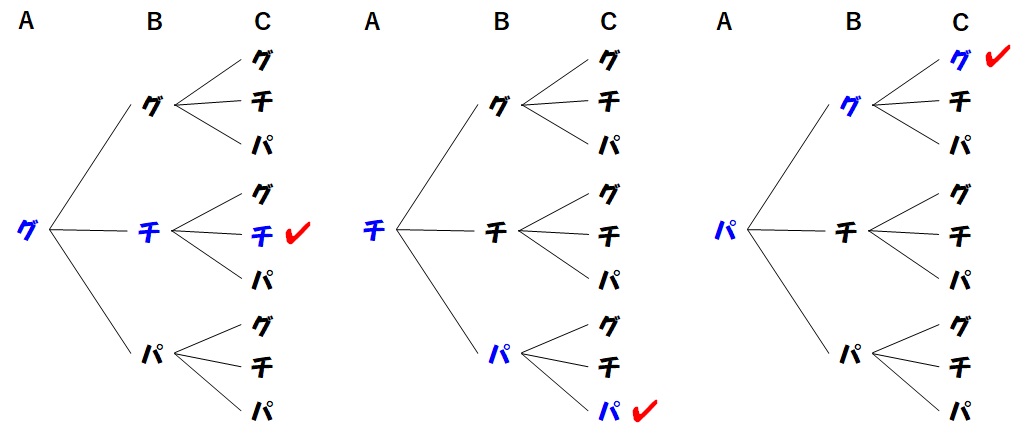
これらの組み合わせの数は3パターンですね。
よって、Aさんだけが勝つ確率は、
$$\text{Aさんだけが勝つ確率} = \frac{3}{27} = \frac{1}{9}$$
となります。
一人勝ちは、あいこよりも確率が低いようです。
問題3:Bさんが勝つ確率を求めよ
続いて、Bさんが勝つ確率です。
注意すべきは、先ほどの問題2では「Aさん一人だけが勝つ」必要がありましたが、今回はBさんが勝てば、その他にAさんかCさんが勝っていてもオッケーという点です。
もちろん、Bさんの一人勝ちもオッケーです。
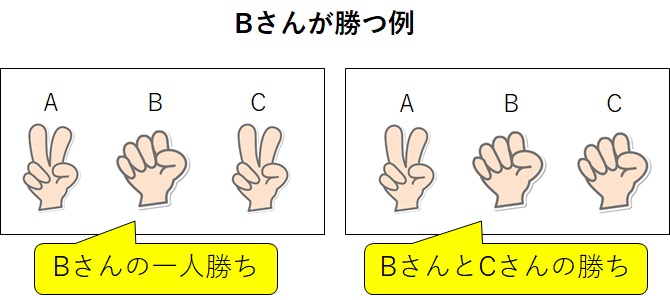
この点は、ちょっとした引っかけ問題として出題されますので、騙されないように覚えておきましょう。
では、樹形図でBさんが勝つパターンにチェックを付けていきます。
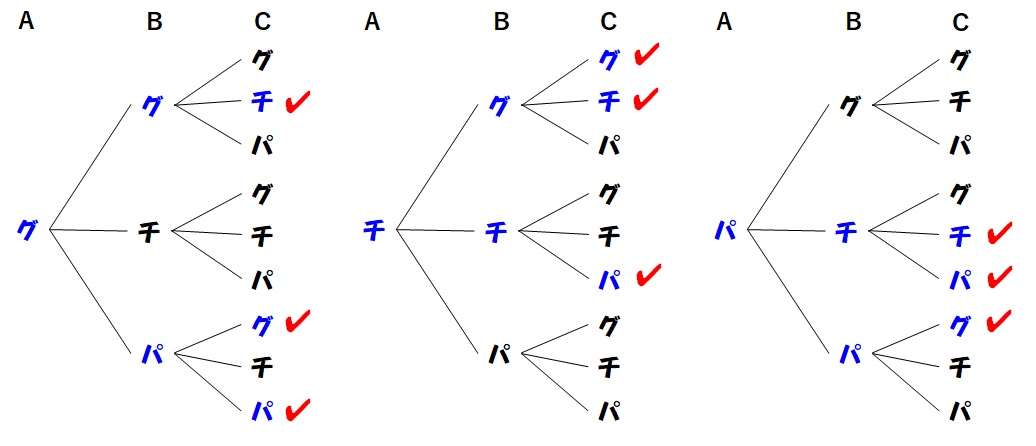
少しわかりづらいので、注意してチェックを付けていっていください。
組み合わせの数は9つです。よってBさんが勝つ確率は、
$$\text{Bさんが勝つ確率} = \frac{9}{27} = \frac{1}{3}$$
となります。
問題4:誰か2人が勝つ確率を求めよ
最後は、誰か2人が勝つ場合です。
AさんとCさんが勝ってもいいですし、BさんとCさんが勝ってもいいです。誰でもいいので、誰か2人が勝つ場合を考えましょう。
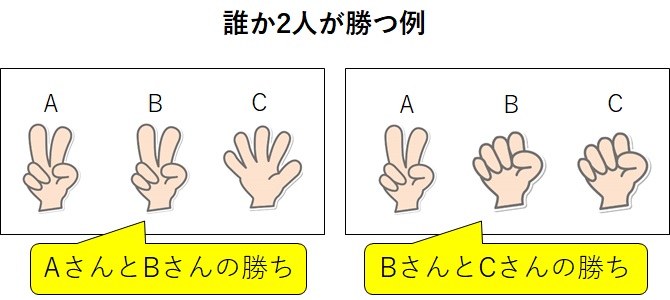
では、これまでと同じように樹形図にチェックを付けていきます。
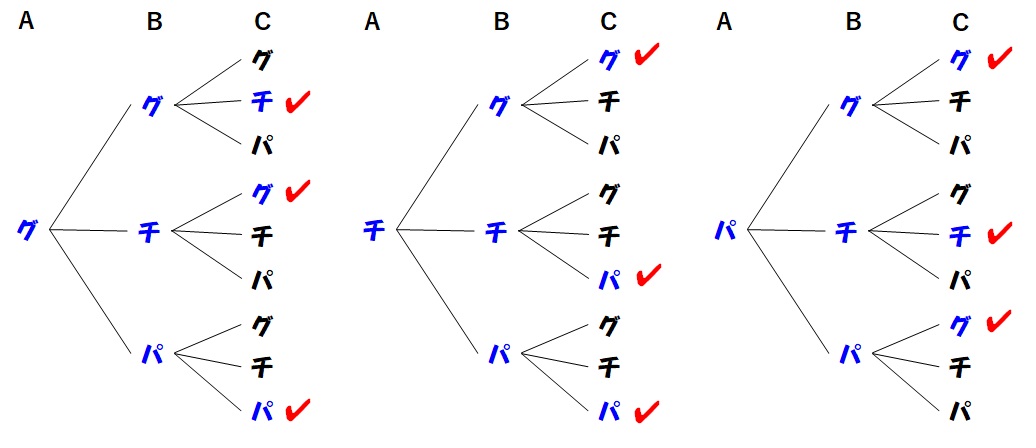
組み合わせの数は9つです。よって誰か2人が勝つ確率は、
$$\text{誰か2人が勝つ確率} = \frac{9}{27} = \frac{1}{3}$$
となります。
おまけのアドバイス
この問題について、「樹形図から2人が勝つパターンを見つけづらかったな」という人はいますか?
そんな人は、このように考えて樹形図からパターンを探してみてください。
「2人が勝つということは誰が1人が負けているはずだから、
1人だけ負けているパターンを探せばいい!」
確かに、上の樹形図で選ばれたパターンは、誰か1人だけ負けているパターンとも言えますね。
このように、少し慣れてきたら、自分なりの解釈で問題を読み替えることもやってみてください。
確率の問題は、難しくなってくると少し視点を変えて考えなければいけないときが出てきます。
「自分なりに問題を解釈しなおすこと」はそのような問題に出会ったときに、発想の転換ができるようになるための良い練習になります。
(おまけ問題)BさんとCさんの2人が同時が負ける確率は?
おまけの問題です。
先ほどの問題と同様に、3人でじゃんけんをしたとき、
「BさんとCさんの2人が同時に負ける確率を求めよ。」
この問題を解くとき、これまでと同じように樹形図にチェックを入れていき、組み合わせの数を数えていけばもちろん解けるのですが、ここでは少し違う考え方をしてみましょう。
先ほど述べたように、問題を少し違う角度から見てみるのです。
問題文にある、
「BさんとCさんの2人が同時に負ける」
という表現を別の表現で言い換えることはできないでしょうか?
そうです。BさんとCさんが負けるということは、「Aさんだけが勝つ」と同じ意味です。
「BさんとCさんの2人が同時に負ける」=「Aさんだけが勝つ」
つまり、Aさんだけが勝つ確率を求めれば、この問題は解けるのです。
これまでの問題を思い出してみましょう。
まさに、問題2が「Aさんだけが勝つ確率」を求める問題でした。
したがって、おまけ問題「BさんとCさんの2人が同時に負ける確率を求めよ」の答えは、問題2と同じ、
「BさんとCさんの2人が同時に負ける」=「Aさんだけが勝つ」=\(\frac{1}{9}\)
となります。
これで、じゃんけんが登場する確率の解説は終わります。
ここで、紹介した問題はこの手の問題の基本の基本になりますので、必ず理解しておくようにしましょうね。
まとめ
「じゃんけん」の問題に限らず、中学校の確率の問題を解くときの基本は、「樹形図」を書くことです。
まずは、それからはじめましょう。
テストでよく出題される「じゃんけん」の問題は、三人でじゃんけんをする場合です。
ここで解いた例題は確実に解けるようになっておきましょう。
さらに余裕がある人は、色々な問題に触れておくことが大切です。それによって、どんな問題にも焦らず対応できるようになります。
ちなみに、じゃんけんの確率について、面白いネタを下の記事で紹介しているので、興味のある人は見てみてくださいね↓



】カードが登場する確率の問題の解き方-100x100.jpg)























ディスカッション
コメント一覧
まだ、コメントがありません