0の0乗ってなんなの? – 0乗だから1になる?
0の0乗は、何になるのでしょうか?
0をいくら掛けても0なので、0でしょうか?
それとも、どんな数字の0乗も1なので、1でしょうか?
ここでは、0の0乗について、まずは数学素人の私が考えてみました。
その後、数学の専門家による0の0乗の解説を紹介します。
0の0乗は1?それとも0? – 自力で考えてみた
\(0\)の\(0\)乗とはなんなのでしょうか?
\(0\)とは”何も無い”という意味です。ですので、
\(0\)の\(0\)乗とは、”何も無いもの”を”何も無いもの”乗する
ということになり、まったくイメージできません。
\(0\)なんじゃないか?
累乗は、その数を何回も掛け合わせるものだと習いました。
例えば、\(2\)の\(3\)乗は、\(2\)を\(3\)回掛け合わせたものです。
$$2^3 = 2 \times 2 \times 2$$
しかし、\(0\)を何回も掛け合わせたところで、それは\(0\)です。
$$0^n = 0 \times 0 \times \cdots \times 0 \times 0 = 0$$
”\(0\)乗”というのがよく分からないが……掛けるものが\(0\)だから答えは\(0\)だ!
$$0^0 = 0$$
\(0\)乗は\(1\)だから\(1\)?
でもちょっと待ってください。
\(0\)乗というのは、どんな数字に対しても\(1\)と定義されると聞いたことがあります。
$$2^0 = 1000^0 = 0.000001^0 = 1$$
なぜ\(0\)乗が\(1\)と定義されるのかは、以下の記事をご覧ください。
ということは、\(0\)に対しても例外はなく\(1\)となるのか?
$$0^0 = 1$$
結局、\(0^0\)は\(0\)なのか、それとも\(1\)なのか、はたまたぜんぜん違う値なのか分かりませんでした。
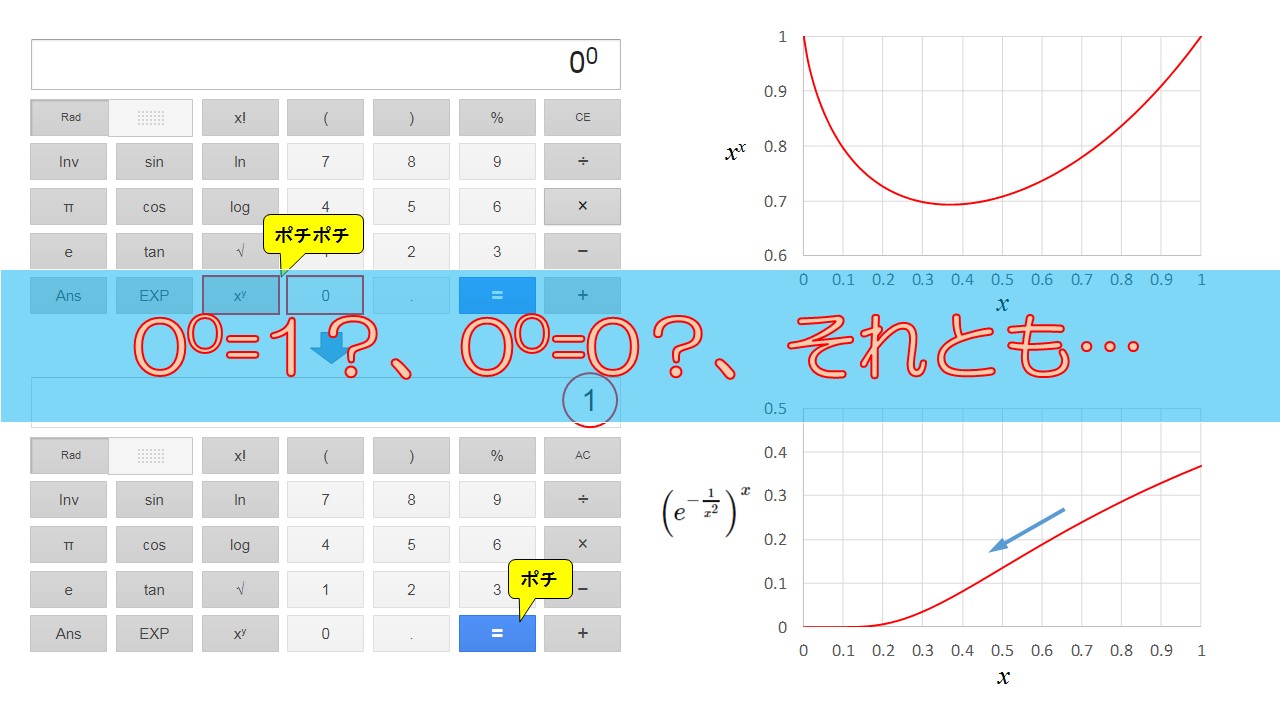
計算機で計算させてみる
電卓で計算する
いろいろ考えても私の頭では分かりそうになかったので、偉大な文明の機器に頼ることにしました。
電卓を使って計算させてみれば一発で答えが出るのではないでしょうか。
さっそく、Google先生のオンライン電卓で計算してみましょう。はじめからやればよかった…
すると下の図のような結果になりました↓
答えは\(1\)です。
やっぱり、\(0^0\)は\(1\)なんですね!
スッキリです。…でも念のため大学生のときに買った関数電卓でも計算させてみました。
すると、

「Math ERROR」?、エラーのようです。
あれっ?Google電卓を信用してよいのか不安になってきました。
エクセルで計算する
次は、エクセルで計算させてみましょう。
結果は以下の通りです。
![]()
「#NUM!」となり、こちらも計算できませんでした。
ならば、正確な\(0\)で計算するのは諦めて、\(0\)ではないがものすごく小さな数で計算させてみましょう。
言うまでもなく、\(1^1\)は\(1\)です。
$$1^1 = 1$$
では、
$$0.1^{0.1}$$
はどうでしょうか?
答えは、
$$0.1^{0.1} = 0.794$$
です。
\(1\)より小さな値となりました。
こんな感じで、値をもっともっと小さくしていけば、限りなく\(0^0\)の値に近い結果が得られるのではないかと考えました。
つまり、
$$x^x$$
の\(x\)を小さくしていく、という考えです。
エクセルでやりましょう。…やりました!
下の図は、\(x\)(横軸)をどんどん小さくしていったときの\(x^x\)(縦軸)の変化を表しています。
ちょっと意外な結果となりました。
\(x=1\)のときは、当然、
$$x^x=1$$
ですが、そこから\(x\)を小さくしていくと、始めは\(x^x\)の値は小さくなっていきます。
さらに小さくしていくと、\(x=0.37\)を下回ったあたりから、今度は\(x^x\)は増加していきます。
そして、\(x^x\)は\(1\)に向かっています。
ということは、
$$\lim_{x \to 0} x^x = 1$$
ということが言えそうです。
「この数式を見たことがない」という人は、
「\(x\)を限りなく\(0\)に近づけていくと\(1\)に向かう」
というふうに考えてください。
やっぱり、
$$0^0 = 1$$
なんだ!
念のために…
私の中では、\(0^0=1\)はほぼ確定なのですが、念のためもう一つだけ検討してみましょう。
上では\(x^x\)の\(x\)を\(0\)に近づけていきました。
しかし、\(0\)に近づくのは\(x\)だけではありません。
例えは、\(\exp{\left( -\frac{1}{x^2} \right)}\)も\(x\)を\(0\)に近づけていけば、\(0\)に向かいます。
\(e\)の肩に乗っている\(-\frac{1}{x^2}\)が\(-\infty\)に向かうからですね↓
$$\lim_{x \to 0} e^{-\frac{1}{x^2}} = 0$$
なので、\(\exp{\left( -\frac{1}{x^2} \right)}\)の\(x\)乗を考えて、\(x\)を\(0\)に近づけていくのもありではないでしょうか?
$$\left( e^{-\frac{1}{x^2}} \right)^x$$
の\(x\)を\(0\)に近づけていきましょう。
結果は、以下のグラフです。
\(x=1\)のとき、\(\left( e^{-\frac{1}{x^2}} \right)^x\)は\(0.36\)あたりから始まっています。
徐々に\(x\)を小さくしていくと、どんどん小さくなっていって最後には、\(0\)になっています。
$$\lim_{x \to 0} \left( e^{-\frac{1}{x^2}} \right)^x = 0$$
ということは、
$$0^0 = 0$$
です。
あれっ?これは前の結果と違います。
\(0^0=1\)になったり、\(0^0=0\)になったりと、もう分からなくなりました。
もう、わたしでは手に負えません。
スポンサーリンク
本格的な「0の0乗」の説明
ここまで色々と私なりに考えてきましたが、結論は、
「よく分からん!」
…ということで、数学専門の方に、
「0の0乗ってどうなんですか?」
と尋ねてみました。
以下からは、数学の専門家による本格的な「0の0乗」の説明です。(今までのはなんだったんだ…)
かなり、丁寧に説明してもらいましたが、かなり上級者向けとなっています。
とにかく、答えだけ知りたいという人は、「まとめ」まで飛びましょう。
※以下、専門家による解説
はじめに
かつて、読売新聞が「\(0\)に\(0\)をかけると\(0\)だが、\(0\)を\(0\)乗すると\(1\)になる・・・」という内容の記事によって、ネットで炎上しているようです。
\(0\)の\(0\)乗とは、\(0^{0}\)と書き、指数関数\(y=a^{x}\)における底\(0\), 指数\(0\)としたものです。
指数関数を高等学校で習うように、実定数\(a\)を固定して、任意の実数\(x\)に対して、\(y\)を\(y=a^{x}\)と定めた時、\(y\)は底\(a\)を持つ指数\(x\)の関数と言います。
\begin{align}
y & = a^x \\
a & : \text{底} \\
x & : \text{指数} \\
\end{align}
ここで重要なのは、\(y=a^{x}\)は、実定数\(a\)が\(a>0\)かつ\(a \neq 1\)の場合のみに定義されているということです。
では、\(0^{0}\)とは、そもそも何かのかを、意味を持つのかを指数関数を復習しながら、検証していきましょう。
指数とは – 簡単に復習しよう
実数\(x\)と自然数\(n\)に対して\(x\)の\(n\)乗とは、\(x\)を\(n\)個かけたものです。
\begin{align}
x^{n}=\underbrace{x \times x \times \cdots \times x}_{n\text{個}}
\end{align}
つまり、
\begin{align}
x^{1}=x, \quad x^{2}=x \times x, \quad x^{3}=x \times x \times x, \quad \cdots, \quad x^{n+1}=x^{n} \times x
\end{align}
のように自然数\(n\)に対して、帰納的に定義されます。
もともと指数とは、同じ数をかけるときに、一回ごとに\(x \times x \times \cdots \times x\)のように書くのを省略するために、表記として用いられたものです。
では、これから、指数を実数の範囲まで拡張してみましょう。
指数の整数への拡張
実数\(x\)と、自然数\(n\)に対して、\(x\)の\(n\)乗とは\(x\)を\(n\)個かけたものを意味しますが、では、\(n\)が自然数ではなく、\(n\)が整数の場合はどのように考えるのでしょうか?
\(n=0\)の場合を考えてみましょう。
\(x^{n+1}=x^{n} \times x\)なので、\(n=0\)を代入すると、\(x^{1}=x^{0} \times x\)となります。
一方で、\(x^{1}=x\)なので、\(x=x^{0} \times x\)となります。
したがって、\(x-x^{0} \times x=0\)なので、
\(x(1-x^{0})=0\)となり、\(x=0\)または\(x^{0}=1\)となります。
ここで注意しなければいけないのが、\(x=0\)のときです。
\(x=0\)のとき、\(x=x^{0} \times x\)に代入すると、\(0=0^{0} \times 0\)となります。
一方で、両辺を\(0\)で割るという操作はできませんが、形式的にかくと、
$$0^{0}=\frac{0}{0}$$
となってしまいます。
\(x \neq 0\)のとき、\(x\)で割るという操作ができるので、\(x(1-x^{0})=0\)について\(x\)で割ると\(x^{0}=1\)となります。
では、\(x\neq 0\)という仮定の下で、整数\(n\)に対して、\(x^{n}\)はどのように振舞うのでしょうか?
\(n>0\)のときは、先ほど見ましたので、\(n<0\)の時を見ていきましょう。
\(m\)を自然数として、\(n=-m\)のとき、
$$1=x^{0}=x^{m-m}=x^{m+(-m)}=x^{m}\times x^{-m}$$
となるので、両辺\(x^{m}\)で割ると、\(x^{-m}=\frac{1}{x^{m}}\)となります。
まとめると、次の公式が得られます。
\(x\)を\(0\)でない実数とし、\(n\)を整数とすると、
$$x^{0}=1, \quad x^{-n}=\frac{1}{x^{n}}$$
となります。
指数の有理数への拡張
先ほど、指数を自然数から整数へと拡張した場合をお話ししました。
また、自然数から整数へ自然に拡張したのと同じように、自然に整数から有理数へ拡張することができます。
そもそも有理数とは何だったのか復習しましょう。
有理数とは、ざっくり言えば、整数\(\div\)整数のことであり、より厳密に集合の形で書くと、
\begin{align}
\left\{ \frac{b}{a} \quad \Big \vert \quad aとbは互いに素な整数でa\neq 0 \right\}
\end{align}
※互いに素:\(a\), \(b\)を共に割り切る正の整数が\(1\)のみであること
と表される集合のことです。
有理数は、整数から次のように自然に構成することができます。
今、整数の集合を\(\mathbb{Z}\)とし、\(\mathbb{Z} \setminus \{ 0 \}\)を整数から\(0\)を除いた集合とします。
任意の2つの元\((m, n), (p, q) \in \mathbb{Z} \times (\mathbb{Z} \setminus \{0 \})\)に対して、二項関係\(\sim\)を\((m, n) \sim (p, q)\)を\(mq=np\)により定義すると、\(\sim\)は、同値関係を満たします。
ここで、同値関係とは、反射律、対称律、推移律の3つの法則を満たすことを言います。
そこで、商集合\((\mathbb{Z} \times (\mathbb{Z} \setminus \{ 0 \}))/\sim\)を有理数の集合\(\mathbb{Q}\)として定義します。
\begin{align}
\mathbb{Q}:=(\mathbb{Z}\times (\mathbb{Z}\setminus \{ 0 \}))/\sim .
\end{align}
このように商集合として有理数を定義することによって、「\(a\)と\(b\)は互いに素」という文言を省くことができます。
この整数から有理数の作り方は、環論における整域とその乗法的部分集合による局所化の構成の一つとして知られています。
整数は、足し算、引き算、掛け算という演算に対して閉じています(このような演算をもつ集合を環と言います)が、有理数は、足し算、引き算、掛け算、割り算という演算について閉じています(このような演算をもつ集合を体と言います)。
今、\(0\)でない実数\(x\)と2つの自然数\(m\), \(n\)で\(m \neq 0\)とした時、\(x^{\frac{n}{m}}\)は何を意味するのでしょうか?
それを説明するために累乗根という概念が必要になります。
\(0\)以上の実数\(x\)と自然数\(n\)に対して、関数\(f(x)=x^{n}\)を考えます。
すると、任意の\(0\)以上の実数\(a\), \(b\)に対して\(a < b\)のとき、\(f(a)=a^{n}<b^{n}=f(b)\)となるので、関数\(f(x)=x^{n}\)は単調増加します。
したがって、\(xy\)平面に置ける曲線\(y=x^{n}\)と直線\(y=a\)との交点はただ一つ存在するので、任意の\(0\)以上の実数\(a\)に対して、\(x^{n}=a\)となる\(0\)以上の実数\(x\)はただ一つ存在します。
この実数\(x\)を\(\sqrt[n]{a}\)と書きます。
\(f(x)=x^{n}\)で\(n\)が偶数のとき、\(xy\)平面に置いて曲線\(y=f(x)\)は\(y\)軸について対称であり、任意の実数\(x\)に対して、\(x^{n} \geq 0\)となります。
\(f(x)=x^{n}\)で\(n\)が奇数のとき、\(xy\)平面に置いて曲線\(y=f(x)\)は原点について対称であり、任意の実数\(x\)に対して、\(f(x)=x^{n}\)は任意の実数値をとる単調増加関数となります。
したがって、\(n\)が偶数かつ実数\(a\)が\(a<0\)のとき、\(x^{n}=a\)は、実数解を持ちません。
これらの理由のため、\(0\)以上の実数\(x\)と\(0\)以上の実数\(a\)と自然数\(n\)に対して、\(\sqrt[n]{a}\)を\(x^{n}=a\)となるただ一つの実数解として定義します。
すると、定義から、\((\sqrt[n]{a})^{n}=a\)が成り立ちます。
では、\(0\)以上の実数\(x\)と2つの自然数\(m\), \(n\)で\(m\neq 0\)とした時、\(x^{\frac{n}{m}}\)は、累乗根を用いて表すことができます。
\begin{align*}
(x^{\frac{n}{m}})^{m}&=\underbrace{x^{\frac{n}{m}}\times x^{\frac{n}{m}}\times \cdots \times x^{\frac{n}{m}}}_{m\text{個}}&\\
&=\underbrace{x^{\frac{n}{m}+\frac{n}{m}+\cdots+\frac{n}{m}}}_{m\text{個}}&\\
&=x^{n}&
\end{align*}
なので、\(x^{\frac{n}{m}}=\sqrt[m]{x^{n}}\)となります。また、\(\sqrt[m]0=0\)です。
まとめると、次の公式が得られます。
\(0\)以上の実数\(x\)と\(2\)つの自然数\(m\), \(n\)で\(m\neq 0\)とした時、
\begin{align}
x^{\frac{n}{m}}=\sqrt[m]{x^{n}}
\end{align}
となります。
指数の実数への拡張
有理数までは、整数から自然に構成することができますが、実数はそこまで簡単というわけではありません。
そこで、この記事では、実数を有理数からCauchyによる方法で構成していきます。
実数の構成
有理数列\(\{a_{n}\}_{n=1}^{\infty}\)がCauchy列であるとは、任意の正の有理数\(\varepsilon\)に対して、ある自然数\(N\)が存在して、任意の自然数\(m, n\)が\(m, n \geq N\)ならば、
\begin{align}
|a_{m}-a_{n}|<\varepsilon
\end{align}
となることを言います。
今、\(\mathbb{A}\)を有理数のCauchy列全体の集合とします。
つまり、
\begin{align}
\mathbb{A}:=\{ \{a_{n} \}_{n=1}^{\infty} : a_{n}\text{は有理数かつCauchy列である。}\}
\end{align}
とします。
任意の2つの有理数列\(\{a_{n} \}_{n=1}^{\infty}, \{b_{n} \}_{n=1}^{\infty} \in \mathbb{A}\)に対してCauchy列であるとき、つまり、任意の正の有理数\(\varepsilon\)に対して、ある自然数\(N\)が存在して、任意の自然数\(m, n\)が\(m, n \geq N\)ならば、
\begin{align}
|a_{m}-b_{n}|<\varepsilon
\end{align}
が成り立つとき、\(\{a_{n} \}_{n=1}^{\infty} \sim \{b_{n} \}_{n=1}^{\infty}\)により二項関係\(\sim\)を定義すると、\(\sim\)は同値関係を満たします。
したがって、\(\mathbb{A}\)の\(\sim\)による商集合\(\mathbb{A}/\sim\)が定義できます。
そこで、\(\mathbb{R}\)を\(\mathbb{A}\)の\(\sim\)による商集合として定義します。
\begin{align}
\mathbb{R}:=\mathbb{A}/\sim.
\end{align}
\(\{a_{n}\}\)の\(\mathbb{R}\)に含まれる代表元を\([a_{n}]\)と表し、任意の2つの元\(\alpha=[a_{n}], \beta=[b_{n}]\in \mathbb{R}\)に対して、足し算を\(\alpha+\beta=[a_{n}+b_{n}]\), 掛け算を\(\alpha\beta=[a_{n}b_{n}]\)により演算を定めると、代表元によらずに、足し算\(\alpha+\beta\), 掛け算\(\alpha\beta\)がただ一通りに決まります。
この足し算、掛け算によって、\(\mathbb{R}\)は体になります。
集合\(\mathbb{R}\)を実数の集合と言い、Cauchy列を使った有理数\(\mathbb{Q}\)から実数\(\mathbb{R}\)への構成方法を完備化と言います。
また、\(a\)が有理数の時は、\(\{a\}_{n=1}^{\infty} =\{a, a, a, \cdots \} \in \mathbb{A}\)の類\([a]\)と同一視します。
元の対応\(a\mapsto [a]\)により、有理数は実数の部分集合として捉えることができます。
また、ある正の有理数\(\varepsilon\)とある自然数\(N\)が存在して、任意の自然数\(n\geq N\)と任意の有理数列\(\{a_{n}\}, \{b_{n}\} \in \mathbb{A}\)に対して、\(a_{n}+\varepsilon<b_{n}\)となる時、\([a_{n}]<[b_{n}]\)と定めると、\(\mathbb{R}\)は数の大小関係\(<\)に関して順序を持ちます。
実数\(\mathbb{R}\)における最も重要な性質は、実数の完備性(もしくは連続性とも言います)です。
つまり、実数列\(\{ \alpha_{n}\}_{n=1}^{\infty}\)がCauchy列であるときに、収束列になることです。
ここで、実数列\(\{ \alpha_{n}\}_{n=1}^{\infty}\)が収束列とは、任意の正の実数\(\varepsilon\)に対して、ある自然数\(N\)とある実数\(\alpha\)が存在して、任意の自然数\(n\)が\(n\geq N\)を満たす時、
\begin{align}
| \alpha_{n}-\alpha|<\varepsilon
\end{align}
となることです。
言い換えると、\(\lim_{n\to \infty}\alpha_{n}\in \mathbb{R}\)ということです。
上記で有理数から実数を構成した方法で、有理数の実数における稠密性、つまり、任意の実数\(a, b\)で\(a<b\)のとき、ある有理数\(r\)が存在して\(a<r<b\)を満たすことを導くことができます。
この証明には、「アルキメデスの原理」という定理が使われます。
ここで、「アルキメデスの原理」とは、任意の2つの正の実数\(x, y\)に対して、\(nx>y\)となる自然数\(n\)が存在するという内容です。
このアルキメデスの原理は、背理法、つまり、\(nx\leq y\)と仮定して矛盾を導き出すことによって、証明ができます。
では、「アルキメデスの原理」を使って、有理数が実数において稠密であることを証明しましょう。
\(a<b\)なので、\(b-a>0\)となり、したがって、アルキメデスの原理によりある自然数\(n\)が存在して、\(n(b-a)>1\)を満たします。
また、アルキメデスの原理より\(m\leq na<m+1\)となる整数\(m\)が存在します。すると、
\begin{align}
nb=na+n(b-a)>m+1>na
\end{align}
なので、両辺を\(n\)で割ると
\begin{align}
a<\frac{m+1}{n}<b
\end{align}
となるので、\(r=\frac{m+1}{n}\)と置けば良いことがわかります。
以上で、有理数\(\mathbb{Q}\)が実数\(\mathbb{R}\)において稠密であることを示すことができました。
また、有理数\(\mathbb{Q}\)が実数\(\mathbb{R}\)において稠密であるということは、任意の実数\(\alpha\)に対して、ある有理数列\(\{a_{n} \}_{n=1}^{\infty}\)が存在して、
\begin{align}
\lim_{n\to \infty}a_{n}=\alpha
\end{align}
になることと同値になります。
この同値性を証明しましょう。
まず、有理数\(\mathbb{Q}\)が実数\(\mathbb{R}\)に稠密なので、任意の実数\(a, b\)で\(a<b\)のとき、ある自然数\(N\)が存在して、有理数列\(\{a_{n}\}_{n=1}^{\infty}\)において\(n\geq N\)を満たす任意の自然数\(n\)に対して\(a<a_{n}<b\)を満たすように取れます。
すると、任意の\(\varepsilon>0\)に対して、\(a=\alpha-\varepsilon\) \(b=\alpha+\varepsilon\)とすれば、
\begin{align}
|a_{n}-\alpha|<\varepsilon
\end{align}
となり、\(\lim_{n\to \infty}a_{n}=\alpha\)が示されました。
逆に、\(\lim_{n\to \infty}a_{n}=\alpha\)を仮定した時、先ほどの証明の逆をたどることによって、有理数は実数において稠密であることも示されます。
また、有理数が実数において稠密であるという事実をさらに次のように精密化して、「実数の十進小数展開」が導かれます。
つまり、任意の実数\(\alpha\)に対して、
\begin{align}
r_{n}=[\alpha]+\sum_{k=1}^{n}\frac{x_{k}}{10^{k}}, \quad 0\leq x_{k}\leq 9,\quad x_{k}\text{は整数}
\end{align}
となる有理数列\(\{ r_{n}\}_{n=1}^{\infty}\)が存在し、\(\lim\limits_{n\to \infty}r_{n}=\alpha\)となります。
ただし、\([\alpha]\)は実数\(\alpha\)を超えない最大の整数を表します。
この「実数の十進小数展開」を証明しましょう。
まず、\(x_{0}=x-[x]\)とおきます。
すると、\(0\leq x_{0}<1\)となります。今、半開区間\([0, 1)\)を次のように十等分します。
\begin{align}
[0, 1)=\bigcup_{k=0}^{9}\left[ \frac{k}{10}, \frac{k+1}{10} \right)
\end{align}
したがって、\(x_{0}\in [0, 1)\)なので、ある整数\(0\leq k\leq 9\)が存在して、\(x_{0}\in \left[ \frac{k}{10}, \frac{k+1}{10} \right)\)となります。
この\(k\)を\(k=x_{1}\)とおきます。
そして、\(\left[ \frac{x_{1}}{10}, \frac{x_{1}+1}{10} \right)\)を次のように十等分します。
\begin{align}
\left[ \frac{x_{1}}{10}, \frac{x_{1}+1}{10} \right)=\bigcup_{\ell=0}^{9}\left[ \frac{x_{1}}{10}+\frac{\ell}{10^{2}}, \frac{x_{1}}{10}+\frac{\ell +1}{10^{2}}\right)
\end{align}
したがって、\(x_{0}\in \left[ \frac{x_{1}}{10}, \frac{x_{1}+1}{10} \right)\)なので、ある整数\(0\leq \ell \leq 9\)が存在して、\(x_{0}\in \left[ \frac{x_{1}}{10}+\frac{\ell}{10^{2}}, \frac{x_{1}}{10}+\frac{\ell +1}{10^{2}}\right)\)となります。
この\(\ell\)を\(\ell=x_{2}\)とおきます。
この十等分の操作を繰り返していくことによって、\(x_{1} , x_{2}, \cdots, x_{n}\)がただ一通りに決まり、そして\(r_{n}\)がこの\(x_{1} , x_{2}, \cdots, x_{n}\)から作られます。
すると、
\begin{align}
x_{0}\in \left[ \sum_{k=1}^{n}\frac{x_{k}}{10^{k}},\sum_{k=1}^{n}\frac{x_{k}}{10^{k}}+\frac{1}{10^{n}} \right)
\end{align}
となるので、整数\([x]\)の大きさだけ平行移動することにより、
\begin{align}
\alpha \in \left[ [x]+\sum_{k=1}^{n}\frac{x_{k}}{10^{k}}, [x]+\sum_{k=1}^{n}\frac{x_{k}}{10^{k}}+\frac{1}{10^{n}} \right)
=\left[ r_{n}, r_{n}+\frac{1}{10^{n}} \right)
\end{align}
となります。したがって、
\begin{align}
0\leq \alpha-r_{n}<\frac{1}{10^{n}}
\end{align}
となり、\(\lim\limits_{n\to \infty}\frac{1}{10^{n}}=0\)なので、はさみうちの原理から
\begin{align}
\lim_{n\to \infty}r_{n}=\alpha
\end{align}
となることがわかります。
具体例として、無理数\(\sqrt{2}\)は、
\begin{align}
r_{1}=1.4,\ r_{2}=1.41,\ r_{3}=1.414,\ r_{4}=1.4142,\ r_{5}=1.41421, \quad \cdots
\end{align}
のように、十進展開ができます。
実数の性質
- 実数は完備性(連続性ともいう)である。したがって、アルキメデスの原理とCauchy列を使った有理数から実数への構成方法から空でない任意の実数の、上に有界な部分集合\(A\)に対して、その上界\(\operatorname{sup}(A)\)は必ず存在することがわかる。
- 有理数は実数において稠密であり、十進展開表示ができる。
指数の実数への拡張
「指数の有理数への拡張」で指数を有理数まで拡張しましたが、今度は実数まで拡張します。
\(x\)を\(0\)以上の実数とし、\(\alpha\)を実数とします。
すると、有理数は実数に稠密なので、ある有理数列\(\{ r_{n}\}_{n=1}^{\infty}\)が存在して、
\begin{align}
\lim_{n\to \infty}r_{n}=\alpha
\end{align}
を満たします。
今、\(f: \mathbb{Q}\rightarrow \mathbb{R}\)を\(f(r_{n})=x^{r_{n}}\)と定めます。
\(\widetilde{f}: \mathbb{R}\rightarrow \mathbb{R}\)を、
\begin{align}
\widetilde{f}(\alpha)=
\begin{cases}
f(r_{n})& \text{$\alpha$が有理数のとき}\\
\lim\limits_{n\to \infty}f(r_{n})& \text{$\alpha$が無理数のとき}\\
\end{cases}
\end{align}
と定めることを目標とします。
その時に、問題点が2つあります。
一つ目は、\(\alpha\)が無理数の時に数列\(\{ x^{r_{n}} \}\)の極限値が存在するかどうかということと、二つめは、\(\alpha\)が無理数の時に数列\(\{ x^{r_{n}} \}\)の極限値がただ一通りで表されるかどうかということです。
まず、\(\alpha\)が無理数の時に数列\(\{ x^{r_{n}} \}\)の極限値が存在するかを見て見ましょう。
実数の構成で見たように、有理数は実数において稠密であり、さらに精密化して、実数の十進小数展開表示ができます。すなわち、任意の実数\(\alpha\)に対して、
\begin{align}
r_{n}=[\alpha]+\sum_{k=1}^{n}\frac{x_{k}}{10^{k}}, \quad 0\leq x_{k}\leq 9,\quad x_{k}\text{は整数}
\end{align}
となる有理数列\(\{ r_{n}\}_{n=1}^{\infty}\)が存在し、\(\lim\limits_{n\to \infty}r_{n}=\alpha\)となります。
今、\(0\)以上の実数\(x\)を\(x>1\)と仮定します。
無理数\(\alpha\)は、上記で見たように有理数列として十進小数展開表示\(\{ r_{n} \}_{n=1}^{\infty}\)が存在し、\(\lim\limits_{n\to \infty}r_{n}=\alpha\)を満たします。
すると、\(\{ r_{n} \}_{n=1}^{\infty}\)は単調増加数列になり、任意の自然数\(n\)に対して\(r_{n}\leq \alpha\)となるので、\(r_{n}\)は上に有界となります。
\(x>1\)なので、数列\(\{ x^{r_{n}}\}_{n=1}^{\infty}\)も単調増加数列となります。
有理数は実数において稠密なので、\(\alpha<\beta\)となる有理数\(\beta\)が存在します。
したがって、\(x^{r_{n}}< x^{\beta}\)となり、数列\(\{ x^{r_{n}}\}_{n=1}^{\infty}\)は上に有界になります。
\(A=\{ x^{r_{n}} : n\text{は自然数} \}\)とおくと、集合\(A\)は\(A\neq \emptyset\)で上に有界なので、実数の連続性により、\(\operatorname{sup}(A)\)が存在します。
したがって、\(\gamma=\operatorname{sup}(A)\)と置くと、任意の自然数\(n\)に対して\(x^{r_{n}}\leq \gamma\)となり、また、任意の\(\varepsilon>0\)に対して、ある自然数\(N\)が存在して、任意の自然数\(n\)が\(n\geq N\)を満たす時、
\begin{align}
x^{r_{n}}>\gamma -\varepsilon
\end{align}
となります。つまり、
\begin{align}
-\varepsilon<x^{r_{n}}-\gamma<\varepsilon
\end{align}
なので、\(|x^{r_{n}}-\gamma|<\varepsilon\)となります。
したがって、
\begin{align}
\gamma=\lim_{n \to \infty}x^{r_{n}}
\end{align}
となります。
以上で、無理数\(\alpha\)に対して、有理数列として十進小数展開表示\(\{ r_{n} \}_{n=1}^{\infty}\)が存在し、\(\lim\limits_{n\to \infty}r_{n}=\alpha\)となるとき、数列\(\{ x^{r_{n}}\}_{n=1}^{\infty}\)の極限値が存在することがわかりました。
次に、\(\alpha\)が無理数の時に数列\(\{ x^{r_{n}} \}_{n=1}^{\infty}\)の極限値がただ一通りで表されるかどうかを見て見ましょう。
言い換えると、2つの有理数列\(\{ p_{n} \}_{n=1}^{\infty}\)と\(\{ q_{n} \}_{n=1}^{\infty}\)で両方とも無理数\(\alpha\)に収束するものを取ってきたとき、数列\(\{ x^{p_{n}} \}_{n=1}^{\infty}\)と\(\{ x^{q_{n}} \}_{n=1}^{\infty}\)の極限値が一致するかどうかを調べてみましょう。
例えば、\(\alpha=\sqrt{2}\)とし、\(\{ p_{n} \}_{n=1}^{\infty}\)を十進小数展開、つまり、
\begin{align}
p_{1}=1.4,\ p_{2}=1.41,\ p_{3}=1.414,\ p_{4}=1.4142,…\cdots
\end{align}
として、\(\{ q_{n} \}_{n=1}^{\infty}\)を連分数展開した有理数列とします。
つまり、
\begin{align}
q_{n+1}=1+\frac{1}{1+q_{n}}, \quad q_{1}=1
\end{align}
とします。
話を戻します。今、\(\{r_{n} \}_{n=1}^{\infty}\)を2つの有理数列\(\{ p_{n} \}_{n=1}^{\infty}\)と\(\{ q_{n} \}_{n=1}^{\infty}\)で現れるすべての項を使って、
単調増加になるような有理数列とします。
すると、\(\lim\limits_{n\to \infty}r_{n}=\alpha\)となり、先ほど見たように、数列\(\{ x^{r_{n}}\}_{n=1}^{\infty}\)は極限値を持ちます。
それを\(\gamma\)と書きます。
すると、2つの数列\(\{ x^{p_{n}} \}_{n=1}^{\infty}\)と\(\{ x^{q_{n}}\}_{n=1}^{\infty}\)は、\(\{ x^{r_{n}}\}_{n=1}^{\infty}\)の部分列なので、2つの数列\(\{ x^{p_{n}} \}_{n=1}^{\infty}\)と\(\{ x^{q_{n}} \}_{n=1}^{\infty}\)も\(\{ x^{r_{n}}\}_{n=1}^{\infty}\)の極限値\(\gamma\)にならなければなりません。
したがって、数列\(\{ x^{p_{n}} \}_{n=1}^{\infty}\)と\(\{ x^{q_{n}} \}_{n=1}^{\infty}\)の極限値が一致することがわかりました。
具体例として、\(2^{\sqrt{2}}\)はどのような数なのかを定義に基づいて考えてみましょう。
まず、有理数列\(\{ r_{n} \}_{n=1}^{\infty}\)を\(\sqrt{2}\)の十進小数展開とします。
言い換えると、\(r_{n}\)を\(\sqrt{2}\)の小数点第\((n+1)\)位以下を除いた数とします。
すると、
\begin{align}
r_{1}=1.4,\ r_{2}=1.41,\ r_{3}=1.414,\ r_{4}=1.4142,\ r_{5}=1.41421,\ \cdots
\end{align}
となり、\(\lim\limits_{n\to \infty}r_{n}=\sqrt{2}\)となります。
すると、数列\(\{ 2^{r_{n}} \}_{n=1}^{\infty}\)は、
\begin{align}
2^{1.4},\ 2^{1.41},\ 2^{1.414},\ 2^{1.4142},\ 2^{1.41421},\ \cdots
\end{align}
となり、それぞれの項の指数は有理数なので、有理数の指数の定義により累乗根を使って計算することができます。
\(\{ r_{n} \}_{n=1}^{\infty}\)は上に有界な単調増加数列なので、\(\{ 2^{r_{n} }\}_{n=1}^{\infty}\)も上に有界な単調増加数列となります。
すると、実数の連続性により、\(\lim\limits_{n\to \infty}2^{r_{n}}\)が存在し、\(2^{\sqrt{2}}=\lim\limits_{n\to \infty}2^{r_{n}}\)と定義することによって、\(2^{\sqrt{2}}\)は意味を持ちます。
\(0< x<1\)の時も、同様に説明することができます。
まとめると、
\(\alpha\)が実数の時に、有理数は実数において稠密なので、ある有理数列\(\{r_{n} \}_{n=1}^{\infty}\)が存在して、\(\lim\limits_{n\to \infty}r_{n}=\alpha\)となります。
特に、\(\alpha\)が無理数のとき、
\begin{align}
x^{\alpha}=\lim_{n\to \infty}x^{r_{n}}
\end{align}
と定義することによって、指数を実数に拡張することができます。
解析学と代数学から見た\(0^{0}\)の意味
解析学から見た\(0^{0}\)と代数学から見た\(0^{0}\)をそれぞれ考えていこうと思います。
代数学から見た\(0^{0}\)の意味
「指数の整数への拡張」で見たように、指数\(n\)が整数のとき、任意の実数\(x\)に対して、
\begin{align}
x^{n+1}=x^{n}\times x
\end{align}
と\(n\)に関して帰納的に定義しました。
\(n=0, x=0\)を代入すると、
\begin{align}
0^{0}=\frac{0}{0}
\end{align}
となってしまいます。
したがって、\(0^{0}\)は\(0\div 0\)と意味します。
\(0\)で割るという操作は、定義されていません。
代数学において、実数は体(たい)をなします。
ここで、体(英: field, 独: K\” {o}rper)とは、集合\(K\)に二つの演算\((+, \times)\)が定められていて、以下の性質を満たすものです。
- 足し算\(+\)に関して、可換群となり、単位元は\(0\)であり、任意の\(a\in K\)に対して、逆元は\(-a\in K\)である。
- 足し算\(+\)と掛け算\(\times\)に対して、分配法則を満たす(\(a\times (b+c)=a\times b+a\times c\))。
- \(K^{\times}\)を\(K\)の可逆元全体の集合とすると、集合として\(K^{\times}=K\setminus \{ 0\}\)を満たす。
- 足し算\(+\), 掛け算\(\times\)という演算について閉じている。
ここで、一般に掛け算\(\times\)に対して、\(a\times b=b\times a\)が成り立つ場合を可換体といい、通常は体と言います。
\(a\times b\neq b\times a\)が成り立つ場合、斜体(英:skew field, 独: Schiefk\”{o}rper)といいます。
Hamiltonの四元数は、斜体として有名な例の一つです。
特に、集合として\(K^{\times}=K\setminus \{ 0\}\)が成り立つという文言を見ると、最初から「\(0\)で割る」という操作が除外されています。
したがって、
代数学では、\(0^{0}\)は\(\frac{0}{0}\)の事であり、「\(0\)で割る」という操作が除外されているので、「\(0^{0}\)は定義しない」もしくは「\(0^{0}\)は存在しない」
というのが、\(0^{0}\)に対する解答です。
解析学から見た\(0^{0}\)の意味
解析学の視点から見ても、実数は実数体としてみなされているので、代数的に定義されなかったのと同様に、\(0^{0}\)は定義されていません。
しかし、便宜上\(0^{0}\)を\(1\)と定義したりすることもあります。
そもそも、\(0^{0}=1\)と定義することによって、どのようなメリットがあるのでしょうか?
まず、二変数関数
\begin{align}
f(x, y)=x^{y}, \quad (x>0)
\end{align}
を考えると、\(f: (0, \infty)\times \mathbb{R} \rightarrow \mathbb{R}\)は連続関数となります。
ここで、考えたいのが
\begin{align}
\lim_{(x, y)\rightarrow (0, 0)}f(x, y)
\end{align}
が存在するかどうかです。
\((x, y)\)を\((0, 0)\)に近づける場合、近づけ方に依存せずに、つまり、\((x, y)\)から\((0, 0)\)までどんな経路をたどっても、\(\lim\limits_{(x, y)\rightarrow (0, 0)}f(x, y)\)がただ一通りに存在すれば、\(f(x, y)$は$(x, y)=(0, 0)\)で連続となります。
では、\((x, y)\)から\((0, 0)\)まで近づける時に、まず直線\(y=x\)に沿って近づけましょう。
つまり、正の方向から$0$に近づける極限値
\begin{align}
\lim_{x\rightarrow 0+}x^{x}
\end{align}
が存在するかどうかを調べます。
\(\lim\limits_{x\rightarrow 0+}x^{x}\)を考えるとき、自然対数\(\lim\limits_{x\rightarrow 0+}x \log(x)\)が存在するか考えます。
ここで、\(t=-\log(x)\)と置くと、\(x=e^{-t}\)となり、\(x\rightarrow 0+\)の時、\(t\rightarrow +\infty\)となります。
したがって、\(\lim\limits_{x\rightarrow 0+}x \log(x)=\lim\limits_{t\rightarrow +\infty}te^{-t}\)となります。
ゆえに、Taylor展開による不等式
\begin{align}
e^{t}\geq 1+t+\frac{t^{2}}{2},\quad (t\geq 0)
\end{align}
より、\(t\geq 0\)に対して、
\begin{align}
0<te^{-t}\leq \frac{t}{1+t+\frac{t^{2}}{2}}
\end{align}
を満たすので、はさみうちの原理から\(\lim\limits_{t\rightarrow +\infty}te^{-t}=0\)となります。
したがって、\(\lim\limits_{x\rightarrow 0+}x \log(x)=0\)となり、\(\lim\limits_{x\rightarrow 0+}x^{x}=1\)となります。
次に、\((x, y)\)から\((0, 0)\)まで近づける時に、曲線\(y=\frac{1}{\log(x)}\)に沿って近づけましょう。
\(\lim\limits_{x\to 0+}\log(x)=-\infty\)なので、\(\lim\limits_{x\to 0+}\frac{1}{\log(x)}=0\)となることに注意します。
\begin{align}
\lim_{x\to 0+}x^{\frac{1}{\log(x)}}
\end{align}
が存在するかどうかを調べます。
先ほどと同様に、自然対数をとると、\(\lim\limits_{x\to 0+}\frac{1}{\log(x)}\cdot \log(x)=1\)となるので、
\begin{align}
\lim_{x\to 0+}x^{\frac{1}{\log(x)}}=e
\end{align}
となります。
直線\(y=x\)に沿って原点に近づける場合と、曲線\(y=\frac{1}{\log(x)}\)に沿って原点に近づける場合と、極限値が異なります。
したがって、\(f(x, y)=x^{y}\)は原点\((0, 0)\)で連続ではありません。
\(0^{0}=1\)と定義すると、\(x>0\)で定義されている関数\(f(x)=x^{x}\)は、\(\lim\limits_{x\rightarrow 0+}f(x)=1\)となるので、\(x=0\)で連続となります。
より一般に実数上の実数値関数\(f(x)\), \(g(x)\)が\(x=a\)で連続かつ\(0\)に近づく場合、すなわち
\begin{align}
\lim_{x\to a}f(x)=0,\quad \lim_{x\to a}g(x)=0
\end{align}
を満たす場合、
\begin{align}
0^{0}=\lim_{x\to a}f(x)^{g(x)}
\end{align}
と定義する場合があります。
しかし、\(f(x)\), \(g(x)\)の選び方によって、値が異なったり、存在しなかったりします。
以上で、解析学から見ると、
\(0^{0}\)は、実数上の実数値関数\(f(x)\), \(g(x)\)が\(x=a\)で連続かつ\(0\)に近づく場合、単なる記号として、\(0^{0}=\lim\limits_{x\to a}f(x)^{g(x)}\)と書く。
ということです。
まとめ
\(0^{0}\)は、代数学の視点で見ると、\(0^{0}=\frac{0}{0}\)となってしまい、\(0\)で割るという操作は定義されていないので、\(0^{0}\)は存在しません。
また、\(0^{0}\)は、解析学の視点で見ると、一つの固定した実数\(a\)に対して、
$$\lim\limits_{x\to a}f(x)=0,\quad \lim\limits_{x\to a}g(x)=0$$
となる関数\(f(x)\), \(g(x)\)に対して、\(0^{0}=\lim\limits_{x\to a}f(x)^{g(x)}\)と記号として便宜上書くことがありますが、極限値として存在するか、存在しないかは\(f(x)\), \(g(x)\)の選び方に依存するということです。






















ディスカッション
コメント一覧
わかりやすかったです
貴方は数学の玄人です
都合のいい決まり事を押し付けないで、下さい。
0✖0は0 1✖1は1です。
指数がどんな数字でも。
どうしてこの説明のほうが、便利なのかを説明して下さい。
?
>どうしてこの説明のほうが、便利なのかを説明して下さい。
ちょっとなにを言ってるのかわからない。
単純な掛け算じゃなくて累乗の話なんだけどなぁ
・・・
Nanisore!