7月22日は円周率の日！なぜ？3月14日じゃなの？

2018年2月10日2020年5月20日

マイナーな円周率の日”7月22日”

最近、友人から聞いたのですが、”円周率の日”というのがあるらしいのです。

円周率と言ったら、数学で一番有名な数”3.14″がすぐに思い浮かびます。

なので、「へぇ～、3月14日？」と言ったら、

「確かに3月14日が一番有名な円周率の日だけど、もう一つあるんだ」

ということです。

聞くと、もう一つの円周率の日は7月22日らしいのです。なぜでしょうか？

初めて聞いたとき、わたしは全くわかりませんでした。以下では7月22日がなぜ円周率の日と呼ばれているのか、その理由を説明します。

 

スポンサーリンク

7月22日が円周率の日の理由

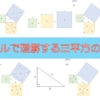
7月22日が第2の円周率の日である理由、それは22を7で割ると、

$$\frac{22}{7} = 3.14285 \cdots $$

となり、答えの初めの三つの数字が”3.14″だから、だそうです。（※ちなみに、円周率は3.141592…なので小数点第3桁以下は違っています）

 

これを聞いて、「なるほどぁ～」と思っていたのですが、ちょっと待ってください！

日を月で割った数が3.14になる日なら7月22日以外にもあるんじゃないでしょうか？

何も7月22日だけを円周率の日としなくてもいいはずです。

 

他の円周率の日も探そう

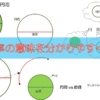
ということで、7月22日以外にも日を月で割った数が3.14になる日付を片っ端から探しました。

エクセルで計算した表を載せます。単純に日を月で割っているだけです。

365日すべての日を探しましたが、3.14となるのは7月22日（表中の赤い日）だけでした。残念、新しい円周率の日は見つかりませんでした。

 

話は少しそれますが、円周率（\(\pi\)）の他に数学でよく登場する定数でネイピア数（\(e\)）というのがあります。この値は、

$$e = 2.718281\cdots$$

なのですが、7月19日（表中の青い日）の日にちを月で割ると2.71からはじまります。なので、7月19日は”ネイピア数の日”、もしくは”eの日”とは言わないのでしょうか…。

わくわくしながら調べてみましたが、そんな日は無いようですね（笑）。

 

ところで、”22÷7″が円周率に近いということは誰が初めに見つけたのでしょうか。

それは、いまから2000年以上前の紀元前250年頃に活躍した数学者アルキメデスです。彼は、初めて計算によって円周率を導いた人物なのですが、そのときに円周率の値としてたどり着いたのが、

$$\frac{22}{7} = 3.14\cdots$$

なのです。22/7は、すごく由緒正しい数だったのですね。

彼がどのようにしてこの数字にたどり着いたのか、興味のある人は以下の記事をご覧ください。

 

スポンサーリンク

三つ目の円周率の日があった？！

ここまで見てきたとおり、3月14日、7月22日は円周率の日として良さそうです。では、これ以外には無いのでしょうか。

少し探してみると、

12月21日も円周率の日

というのを見つけました。

説明によると、12月21日は1月1日から数えて355日目だそうです。そして、355を113で割ると、

$$\frac{355}{113} = 3.14159292\cdots$$

となります。円周率(3.141592654…)ですのでかなり小さな小数桁まで合っていますね。これが12月21日が円周率の日である理由だとか…

• どっから113は来たんだ！
• 133日目の4月11日じゃダメなのか？
• こんなんまで言い出したら一年中、円周率の日になってしまうわ！

など言いたいことはたくさんあるかもしれませんが、ここでは「円周率の日は、

• 3月14日
• 7月22日
• 12月21日

の三日である」とまとめさせてください。

 

円周率の日はプロポーズしたり、カップルが籍を入れたりすることも多いみたいです。

円周率が永遠に終わらない数だから、縁起がイイ数なんですね。

 

まとめ

• 円周率の日は”3月14日”、”7月22日”、”12月21日”である
• 7月22日は日にちを月で割ると、3.14が現れるから
• 12月21日は一年間の355日目であり、355/113が円周率に近い値になるからである
• 円周率の日は、縁起がいい日でプロポーズしたり籍を入れたりする日として人気