円周率の意味って何？ – πの意味を分かりやすく説明します

2018年2月10日2020年5月20日

円周率はなんで3.14なのか？その意味は？

まずは”円周率”という漢字に注目しましょう。これが円周率の意味を表してします。

一文字目は”円”です。円周率とは、円と関係があるもののようです。

二文字目は”周”です。”円の周り”ということですね。一文字目も含むと”円周”です。円の周りの長さとの深い関係がある数字であるということが分かります。

最後に”率”です。率とは比のことです。円周の長さを何かと比べることで出てくる値ということですね。

ここまでで分かったことをまとめると、円周率は

• ”円”と関係がある
• その中でも”円周”の長さと深い関係を持つ数である
• 円周の長さを何かと比べたときに出てくる値である

ということです。

「このくらいもう知ってるよ」と思われるかもしれませんが、これらは円周率の意味を理解する上で非常に重要なことですので、もう一度確認しておきましょう。

 

スポンサーリンク

円周率を公式から説明

円には、円周と直径があります。

小学校で円周率\(\pi\)を初めて習ったとき、何となく公式を暗記したと思います。一番初めに登場する円周率を使った公式は、円の円周の長さを求める公式で、

$$\text{円周の長さ} = \pi \times \text{直径}$$

というものでした。この公式は

円周の長さは、円周率に円の直径をかければ求まりますよ

と言っていますね。

でも、これは円周率の本当の意味を隠してしまっているんです。円周率の本当の意味を理解するには、上の式を次の式のように変形します。上の式で両辺を”直径”で割るだけです。

$$\pi = \frac{\text{円周の長さ}}{\text{直径}}$$

この式は、

円周の長さを円の直径で割った数が、円周率ですよ

という意味になりました。

円周の長さを直径で割っているということは、言い換えると、

円周の長さは、直径の何倍ですか？それは、”円周率(3.14)”倍です

ということです。これが円周率の本当の意味なのです。どうでしょうか？

円周率の”率”とは、”円周と直径を比較したときの比率”という意味だったのです。

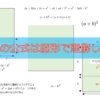
「式で説明されても、いまいちイメージがわかないよ」という人は、次に実際に図形を使って説明してみましょう。

より、視覚的に理解できるはずです。

 

円周率を図形を使って説明

まず、円を描いてみます。

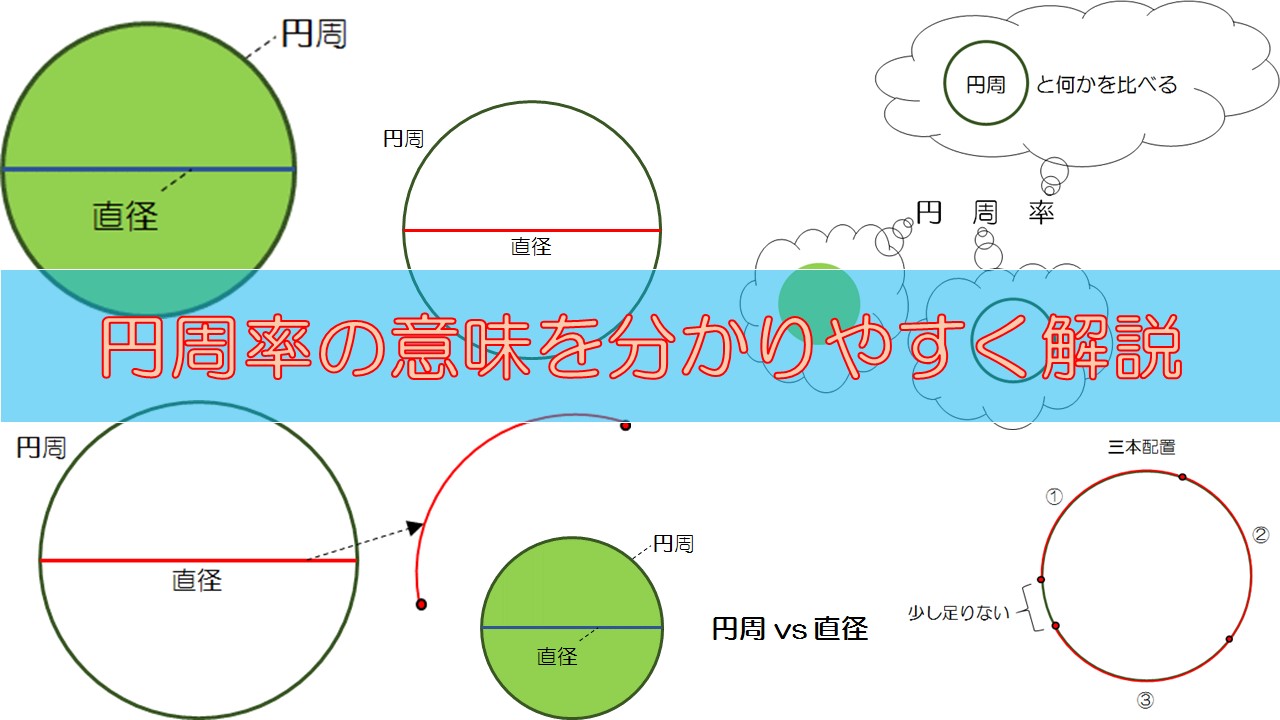
直径と円周を見比べてみましょう。どちらが長そうですか？円周の方が直径よりも長そうですようね。

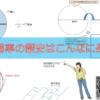
実際に比較してみるために、直径を円周に合わせて曲げます。

このとき、曲げても長さは変わらないですよ。

この状態にして、円周の周りに直径が何本入るかを数えていきましょう。

上の図のように三本配置したところで、あと少し足りない状態になりました。つまり、”円周の長さは、直径の3倍と少し”であるということが分かりました。

では、”少し”とはどのくらいでしょう。それは、直径の0.14倍です。

よって、

円周の長さは、直径の3倍と残り0.14倍である、すなわち3.14倍である

ということです。

円周は直径の何倍であるか？それは3.14倍であり、これを円周率と呼んでいるのです。

これが円周率3.14の意味なのです。

 

スポンサーリンク

正確には3.14じゃない？

円周率は3.14であると覚えますが、正確には3.14ではありません。正確には、

3. 1415926535897932384626433832795028841971…

と永遠に続きます。

この数字は終わりがないことが知られており、現在ではスーパーコンピューターを使って何兆桁まで値が分かっています。

しかし逆に考えると、人類は、

円周の長さは、直径の何倍であるか？

という単純な問題の答えを知らないのです。

面白いですね。ちなみに、円周率は数学史上、もっとも歴史の長い問題です。円周率の誕生は今から約4000年前の紀元前2000年古代バビロニア時代まで遡ります。

昔の人たちはパソコンなんてありませんでした。そんな時代にいったいどうやって円周率を計算していたのでしょうか。興味のある方は、ぜひ以下の記事をご覧ください。面白い円周率の歴史がありますよ。

 

まとめ

• 円周率の意味は、”円周の長さは直径の何倍であるか”ということ
• それは、3.14倍
• 円周の長さを求める公式を変形すると、本当の意味が見えてくる
• 実際に円を描いてイメージすると理解しやすい
• 円周率の値は、本当は3.14ではない