小学生でもできる円周率の求め方 – いろいろな方法を紹介

2018年8月27日2020年1月14日

円周率とは

ここでは、小学生でもできる円周率の求め方をいくつか紹介します。

 

しかし、その前にまず、

「円周率とは何なのか？」

をきちんと理解しておきましょう。

 

円周率とは、

「円の直径と円の周りの長さの比」

です。

上の図の\(C\)は円周の長さ、\(R\)は円の直径です。

そして、円周率はそれらの比であることがわかります。

 

そして、重要なポイントは、

円周率の値は円の大きさによらず、どんな大きさの円でも値が同じである

ということです。

その値は言わずもがな、\(3.14…\)ですね。

 

これをきちんと知っておけば、いろんな円周率の求め方が思いつくと思いますよ。

 

スポンサーリンク

小学生でもできる円周率の求め方とは

ここから先は小学生でもできる円周率の求め方・測り方を紹介していきます。

”小学生でもできる”という意味は、”数学の知識を使わないで求める”ということです。

 

小学生は複雑な数式や図形などの数学の知識をまだ習っていません。

それは中学校から始まる数学の範囲だからです。

 

ここでは、円周率をそんな難しい数学の知識を使わずに求めてみようということです。

 

方法①：ヒモと定規を使った円周率の求め方

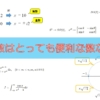
上で解説したように円周率とは、

$$\text{円周率} = \frac{\text{円周の長さ}}{円の直径}$$

でした。

 

ですので、右辺の「円周の長さ」と「円の直径」がわかれば、左辺の円周率を求めることができます。

ここでは、ヒモと定規を使って、

• 円周の長さ
• 円の直径

を求める方法を試してみましょう。

 

まずは、身近にあるもので円の形をしたものを用意しましょう。

なんでもオッケーなのですが、測定の時にやりやすいように、少し厚さのあるものがより良いです。

私は以下のような瓶のふたを見つけました。

この円の、「直径」と「円周の長さ」を測ればよいです。

 

直径を測る

まずは、簡単に定規で測れる「直径」から測ってみましょう。

下の図のように定規をフタの上に置き、直径を測りましょう。

私の場合は、11.2cmとなりました。

円の直径 = 11.2cm

 

測るときのコツは、

”とにかく一番長くなる場所を見つけること”

です。

その理由は、円の特徴として、円上のどこか2点を結んだとき一番長くなる2点を結んだ長さが直径となるからです。

ですので、少しずつ定規を動かしてみて、一番長くなる位置を見つけてから、定規の目盛りを読みメモしましょう。

 

円周の長さを測る

さて、次は円周の長さを測りましょう。

しかし、問題は円は曲線なので定規では測れないということです。

 

こんなときは、ヒモを使います。

適当なヒモを用意して、円の円周に巻いていきます。

厚みのあるものを用意して欲しいといったのはこのためです。ヒモが巻きやすいですよね。

1周巻いて印をつけたら、ヒモを伸ばし長さを定規で測っていきましょう。

これで、円の円周の長さがわかりました。

私の場合、

円周の長さ = 35.9cm

でした。

 

円周率の式にあてはめる

ここまでで、円周率を求めるために必要な情報、

• 円の直径 = 11.2 cm
• 円周の長さ = 35.9 cm

がわかりました。

 

あとは、円周率の式、

$$\text{円周率} = \frac{円周の長さ}{円の直径}$$

に測定した長さを代入して計算します。

\begin{align}
\text{円周率} & = \frac{円周の長さ}{円の直径} \\
& = \frac{35.9}{11.2} \\
& = 3.205
\end{align}

 

これより、私が求めた円周率は\(3.205\)となりました。

正しい円周率は\(3.14\cdots\)ですので、そのズレは\(0.065\)です。

誤差は2%程度であり、そこそこの結果ではないでしょうか。

 

スポンサーリンク

方法②：たくさんの三角形から円周率を求める

続いての方法は、少し変わっていて面白い方法です。

こんどは、紙とペンと定規、そして円形をしたものを用意しましょう。

これらを使って、円周率を求めるため必要な情報である、

• 円周の長さ
• 円の直径

を求めてみましょう。

 

円に線を引いていく

まずは、円形のものから縁取りをして、紙に円を描きます。

これは、コンパスを使って描いても構いません。

次にこの円を8等分にします。

このとき、厳密に8等分する必要はありません。

だいたい8つに分ければそれでオッケーです。

 

次に、等分した線と円の交わった点を結びます。

すると、8つの三角形ができますね。

 

続いて、円の外側に対しても線を引いていきましょう。

まずは、円を囲む大きな三角形を作りましょう。

さらに、下の図のように円に接する三本の線を追加します。

 

お疲れ様です。これですべての線が引けました。

 

線の長さを測る

ここで、完成した図の線の中で下の図に示した色線に注目してください。

赤い線が円です（円周）。

そして、その円を囲んでいるのが青い線です。

緑の線は円の内側にある線です。

 

ここで、線の長さの大小関係を考えてみましょう。

青い線は、円の円周の長さよりも長そうです。

そして、緑の線は円周の長さよりも短そうです。

 

つまり、線の長さの大小関係は、

緑の線　＜　円周（赤い線）　＜　青い線

となっています。

円周は測るのが難しそうですが、直線で構成されている緑の線と青い線は簡単に定規で測れそうですね。

測ってみましょう。

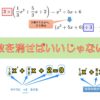
\begin{align}
\text{内側の線の長さ} = 4.4 + 4.3 + 4.2 + 4.4 + 4.4 + 4.4 + 4.3 + 4.5 = 34.9 \text{cm} \\
\text{外側の線の長さ} = 6.0 + 5.9 + 7.2 + 7.8 + 6.8 + 6.3 = 40 \text{cm} \\
\end{align}

 

このような結果となりました。

ということは、これらの長さの間に円周の長さが入ることになりますね。

\(34.9\text{ cm}\)　＜　円周の長さ　＜　\(40\text{ cm}\)

 

このように円周の長さの範囲が絞れたのですが、正確な長さは分かりません。

ですので、ここではだいたい内側の線と外側の線の長さの平均として考えておきましょう。

$$\text{円周の長さ} = \frac{34.9 + 40}{2} = 37.45$$

 

これで円周の長さは求まりました。

 

直径を測る

次は、円の直径を調べましょう。

これは簡単ですね。

定規を使って円の直径を直接測ればオッケーです。

結果は、

$$\text{円の直径} = 11.5\text{ cm}$$

でした。

 

円周率を導出する

これで、準備が整いました。

もう一度、ここでで得た情報を書くと、

• 円の直径 = 11.5 cm
• 円周の長さ = 37.45 cm

です。

これらを円周率の式に入れて計算すると、

\begin{align}
\text{円周率} & = \frac{円周の長さ}{円の直径} \\
& = \frac{37.45}{11.5} \\
& = 3.257
\end{align}

となり、円周率は\(3.257\)と推定されました。

 

正確な円周率である\(3.14\)とは約0.115のズレがあり、初めに紹介したヒモを使って円周を測定する方法よりも少し悪い結果になってしまいましたね。

それでも、誤差は3.7%とまずまずの結果ではないでしょうか？

 

精度を上げたい場合は、もっと細かく多くの三角形を作り、正確に円周の長さを測定すればよいでしょう。

 

方法③：針を投げるだけで円周率が求まる？！

最後に紹介するのは、とっても不思議で面白い方法です。

それは、

「平行な線に棒を投げて円周率を求める」

という方法です。

このとき、投げる棒の長さは平行な線の間隔の半分である必要があります。

 

何度も何度も棒を投げ、”投げた回数”とその時に”棒が平行な線に交わった回数”をカウントします。

 

とにかくたくさん投げましょう。

 

そして、

• 棒を投げた回数
• 棒が平行な線に交わった回数

を数えた後、”棒を投げた回数”を”棒が平行な線に交わった回数”で割ります。

$$\frac{\text{棒を投げた回数}}{\text{棒が平行な線に交わった回数}}$$

実は、この値が円周率になります。

 

たくさんの棒を投げれば投げるほど、精度の高い円周率を得ることができるでしょう。

 

これは「ビュフォンの針実験」と呼ばれるもので、この試行を繰り返していくと数学的に\(\pi\)に近づいていくことが分かっています。

数学的な解説は以下の記事で丁寧に行っていますので、興味のある方はご覧ください。

 

しかし、どのくらいの回数投げればいいのでしょうか？

それを知るために、以下には過去の人たちがどのくらい投げてきたのかを紹介します。

 

過去にいっぱい投げた人ランキング

ビュフォンの針実験は18世紀にフランスの数学者ビュフォンによって考案された実験です。

その後、たくさんの人がビュフォンの実験を行いました。

 

そして、たくさん投げた人ランキングは下の表のようになります。

ランキング	名前	年	投げた回数	導いた円周率
5	フォックス大尉	1864	1030	3.1595
4	レイナ	1925	2520	3.1795
3	スミス・ダベルディーン	1855	3204	3.1553
2	ラッツァリーニ	1901	3408	3.1415929
1	ウルフ	18??	5000	3.1596

一番多く投げたのは、ドイツ・チューリッヒ出身の数学者ウルフさんです。

その回数はなんと5000回！暇人ですね。

そうして得られた円周率は\(3.1596\)です。なかなかの精度ですね。

 

ランキング5位は、フォックス大尉の1030回です。

それでも円周率は\(3.1595\)と悪くない精度です。

 

夏休みなら1000回ぐらいは投げれそうですね。

ぜひ挑戦してみてください。目指せウルフ越え！！

 

スポンサーリンク

まとめ

• 数学の知識を使わず、小学生でもできる円周率の求め方を紹介してきました。
• ここで紹介したのは以下の3パターンの方法です。
  ①ヒモと定規を使って、円周の長さと直径を測り、円周率の式に代入して求める
  ②円の内側と外側に線を引き、円周の長さを推定して円周率の式に代入して求める
  ③平行な線に棒を投げる行為を繰り返して、円周率を求める