虚数の意味や面白い性質を紹介
虚数って何か意味あるの？
実数係数の一次方程式を解くときは、その解は、必ず実数ですよね。
しかし、二次方程式を解くと、判別式が0より小さい時、その解は虚数となります。
虚数の解とは、一体何を意味するのか?
二乗して0より小さい数とは、一体なんなのかイメージが湧きにくいと思います。
この現実(実数)の世界に存在しない数を学んで一体なんの意味があるのか、複素数は一体
なんの役に立つのかを解説していきます。
スポンサーリンク
虚数とはそもそも何か?
虚数とは英語でimaginary number（イマジナリーナンバー）といって、想像上の数というものです。
特に、\(i=\sqrt{-1}\)は虚数単位といって、これを2乗すると、
$$i \times i = -1$$
となります。
2乗するとマイナスになる数とはイメージがわかないですよね。
虚数は、この現実の世界には、存在しない数なのです。
複素数はとは何か?
この虚数単位が入った数を複素数といいます。
複素数全体の集合\({\bf C}\)は、
$${\bf C} = \{ a+bi \ | \ a, b\text{は実数}\}$$
と定義され、足し算に関して、
$$(a+bi)+(c+di)=(a+c)+(b+d)i$$
と定めると、\({\bf C}\)は足し算に関して、加法群の構造を持ちます。
「加法群の構造を持つ」というのは、具体例として、整数からなる集合\({\bf Z}\)に足し算という演算\(+\)を入れると、結合法則、単位元\(0\)が存在し、整数\(a\)の逆元は\(-a\)となり、（この3つの性質を群と言います。）さらに、整数\(a, b\)にたいして\(a+b\)も整数となる（\(+\)について閉じていると言います。）ので、\({\bf Z}\)は足し算という演算\(+\)に対して、群の構造をもつと言います。
ざっくり言えば、足し算と引き算ができる集合のことを加法群と言います。
体(たい, 英語ではfield)というのは、足し算、引き算、掛け算、割り算ができる集合の事です。
したがって、複素数全体の集合\({\bf C}\)は、加法群として二次元実ベクトル空間\({\bf R}^2\)と\({\bf C} \rightarrow {\bf R}^2, \quad a+bi \mapsto (a, b)\)と対応させることによって、同一視することができます。
そして、複素数の掛け算を、
$$(a+bi) \cdot (c+di) = ac – bd + (ad + bc)i$$
複素数\(a+bi\) (\(a\), \(b\)も共に\(0\)ではない実数)の逆数を、
$$\frac{1}{a+bi} = \frac{a-bi}{a^2+b^2}$$
と定義すると、複素数全体の集合\({\bf C}\)は、可換体の構造を持ちます。
つまり四則混合の計算が可能な集合となるのです。
しかし、実数\({\bf R}^2\)とは異なり、実数\({\bf R}^2\)の大小関係の延長である数の大小関係に関して順序を持ちません。
簡単に言えば、例えば、\(\sqrt{-1}\)が、\(0\)より大きいのかそれとも小さいのかを議論することができないということです。
それを簡単に見てみましょう。背理法を使って見てみます!
つまり、\(\sqrt{-1}\)が、\(0\)より大きい（もしくは小さい）と仮定し、矛盾を導きます。
$$\sqrt{-1} > 0$$
と仮定すると、両辺に\(\sqrt{-1}\)をかけると、不等号の向きが変わらないので、\(-1>0\)となり、矛盾します。
また、
$$\sqrt{-1} < 0$$
と仮定すると、両辺に\(\sqrt{-1}\)をかけると、不等号の向きが変わり、\(-1>0\)となり、矛盾します。
また、\(\sqrt{-1} \neq 0\)なので、\(\sqrt{-1}\)は、\(0\)より大きくも小さくもなく、\(\sqrt{-1}\)と\(0\)との大小関係の比較ができないということを意味します。
以上で、複素数は二次元実ベクトル空間であり、実数における数の大小関係の延長における数の大小関係に関して、複素数は順序を持たないことがわかりました。
スポンサーリンク
複素数を可視化するために複素数平面が導入された
複素数は現実世界には存在しないので、可視化することができません。
そこで、ガウスは、19世紀の前半に、複素数平面というものを導入し、複素数を二次元平面（xy平面に置けるx軸を実軸に、y軸を虚軸）にすることによって、複素数を可視化しました。
複素数の代数演算は、複素数平面上で考えると理解しやすいです。
上記で述べたように複素数は二次元実ベクトル空間と同一視できますが、これはあくまでも、足し算・引き算(加法・減法)についてであり、複素数の足し算・引き算(加法・減法)は、二次元実ベクトルの足し算として捉えることができます。
二次元実ベクトル空間では、掛け算は定義されていないので、複素数の掛け算、特に\(\sqrt{-1}\)を掛けるとは一体何を意味するのか、疑問が出てきます。
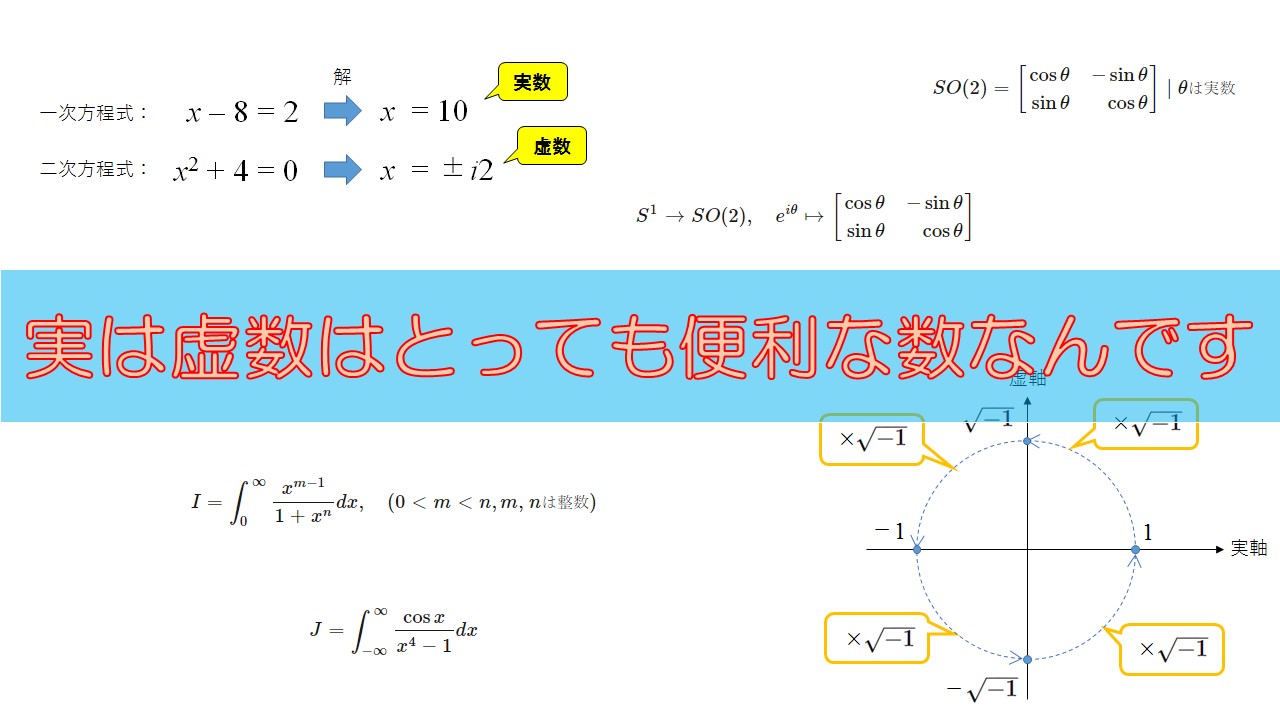
複素数平面において、\(1\)という実数は実軸にあります。
\(1\)に\(\sqrt{-1}\)を掛けると、\(\sqrt{-1}\)は虚軸にあります。
そして、もう一度\(\sqrt{-1}\)をかけると、\(-1\)になり、それは実軸にあります。
さらに、もう一度\(\sqrt{-1}\)をかけると、\(-\sqrt{-1}\)になり、虚軸にあります。
そして、最後にもう一度\(\sqrt{-1}\)をかけると\(1\)となり、元の位置に戻ります。
つまり、
\(\sqrt{-1}\)は、複素数平面では、\(\pi/2\)回転(\(90^{\circ}\)回転)
を意味します。
このように複素数平面を考えることにより、複素数の代数演算は幾何学的操作として捉えることができます。
ではより一般に、複素数平面における複素数\(a+bi\)（\(a, b\)は実数）を掛けるとは一体何を意味するのでしょうか？
複素数の乗法は、実数倍して回転を表す
複素数\(a+bi\) (\(a, b\)は実数)を掛けるとは、複素数平面では、何を意味するのでしょうか?
複素数の掛け算は以下のようになります。
$$(a+bi) \cdot (c+di) = ac-bd+(ad+bc)i$$
この式では複素数平面では何を意味しているのかわかりかねます。
そこで、\(a+bi\)のように直交座標系で表すのではなく、極座標系で見てみることにします。
まず、複素数\(a+bi\)の絶対値を、
$$|a+bi|=\sqrt{a^2+b^2}$$
と定義します。
もともと絶対値とは、数直線で考えると、原点からの距離でした。
従って、複素数の絶対値も、複素数平面における原点からの距離という意味で捉えると、上の定義
は妥当だということがわかります。
そして、原点から点\(z=a+bi\)まで引いた線分と実軸とのなす角度を\(\theta\)とすると、この\(\theta\)を偏角といい、\(\theta=\arg(z)\)としばしば表されます。
すると、点\(a+bi\)は、\(r=\sqrt{a^2+b^2}\)とおくと、\(a=r \cos \theta, b=r \sin \theta\)と書くことができます。
まとめると、
$$a+bi = r (\cos\theta+i\sin\theta) = r e^{i \theta}$$
と書くことができます。
ただし、
$$r = \sqrt{a^2 + b^2}, \quad \cos{\theta} = \frac{a}{\sqrt{a^2+b^2}}, \quad \sin{\theta} = \frac{b}{\sqrt{a^2+b^2}}$$
です。
ここで、\(e^{i \theta} = \cos\theta+i\sin\theta\)は、オイラーの公式と言われ、指数関数と三角関数が虚数によって関係式が得られるという公式です。
複素数\(z\)が\(z=re^{i\theta}\)と極座標で表される時、極座標で表された複素数\(w=\rho e^{i\phi}\)を掛けると、
$$zw = r \rho e^{i(\theta + \phi)}$$
となるので、複素数\(w=\rho e^{i\phi}\)を掛けるという意味は、実数\(\rho\)をかけて、\(\phi\)回転するという意味になります。
スポンサーリンク
複素数の加法と乗法は代数的にどんな意味を持つか
複素数の加法は、群をなし、二次元実ベクトル空間と同一視されます。
より厳密に言えば、複素数の加法群は、二次元実ベクトル空間と代数的に同型となります。
では、複素数の乗法は、一体どのように表されるのでしょうか?
複素数の乗法は、「複素数の乗法は、実数倍して回転を表す」で述べたように、実数倍（拡大・縮小）して、回転を表します。
つまり、線形代数の言葉で言うと、\(2 \times 2\)の回転行列の実数倍として表されます。
今、\(SO(2)\)を\(2 \times 2\)の直交行列全体の表す集合とします。
つまり、
\begin{align}
SO(2) = \left[
\begin{array}{rrr}
\cos{\theta} & -\sin{\theta} \\
\sin{\theta} & \cos{\theta} \\
\end{array}
\right] \mid \theta \text{は実数}
\end{align}
とします。すると、\(SO(2)\)は行列の乗法に関して群をなします。複素数の乗法群を\(\Theta\)として、\(S^1 = \{ z \in \Theta \mid \mid z \mid = 1 \} = \{ z \in \Theta \mid z = e^{i \theta} (\theta \in {\bf R}) \} \)とすると、次の対応を得ます。
\begin{align}
S^1 \rightarrow SO(2) , \quad e^{i \theta} \mapsto \left[
\begin{array}{rrr}
\cos{\theta} & -\sin{\theta} \\
\sin{\theta} & \cos{\theta} \\
\end{array}
\right]
\end{align}
つまり、単位円は2×2の直交行列全体の表す集合\(SO(2)\)と同一視することができます。
より厳密に言うと、単位円は2×2の直交行列全体の表す集合\(SO(2)\)と代数的に同型となります。
以上で、複素数の加法群は二次元実ベクトル空間と代数的に同型であり、複素数の乗法群は2×2の直交行列全体に実数倍したものと代数的に同型であるということがわかります。
複素数ならではのメリット
複素数を学んで一体何のメリットがあるのか、それは、実数では成り立たない概念が複素数では成り立ってしまうこと、実数だけでは計算が難しいものでも複素数では計算がしやすくなったりと、具体例をあげていきます。
例１
実数上で定義された実数値関数、
\begin{align}
f(x) = \left\{
\begin{array}{l}
e^{-\frac{1}{x}} \quad & \text{if} \quad x > 0\\
0 \quad & \text{if} \quad x \leq 0
\end{array}
\right.
\end{align}
を考えると、\(f(x)\)は\(x=0\)で何回も微分可能ですが、\(x=0\)でTaylor展開はできません。
しかし、複素数上では違ってきます。
複素数上の関数\(f(z)\)が複素数値\(z=a\)で微分可能ならば、\(f(z)\)は\(z=a\)でTaylor展開可能となります。
これを保証しているのが、複素解析を学習することによって、学ぶ有名なCauchyの積分公式です。
\({\bf D}\)を複素数平面に置ける連結開集合(領域)とし、\(f\)を\({\bf D}\)上微分可能な複素数値関数\({\bf E} \subset {\bf D}\)、を閉円板とし、\(\hat{\bf E}\)を\({\bf E}\)の内点の集合とし、\(\partial {\bf E}\)を\({\bf E}\)の正の向きの境界とした時、次の公式をCauchyの積分公式と言います。
$$f(z) = \frac{1}{2 \pi i} \int_{\partial {\bf E}} \frac{f(\zeta)}{(z – \zeta)} d \zeta \quad (\forall_Z \in \hat{\bf E})$$
例2
\(n\)次代数方程式は、複素数上まで考えると、複素数上で重根を込めて\(n\)個の複素数解を持つという代数学の基本定理があります。
言い換えると、\(f(z)\)を複素数係数の\(n\)次方程式とした時、\(f(\alpha)=0\)となる複素数\(\alpha\)が存在します。
実数上ではこの定理は成り立ちません。
この定理は、複素解析を学習すると、上に有界な正則関数(微分可能な複素数上の関数)は定数に限るというLiouvilleの定理とか、偏角の原理とか、Roucheの定理などの様々な定理を利用しすることによって、証明することができます。
代数方程式を解くときに、複素数の範囲で考えたほうが、重複を許して一次式の掛け算として、因数分解できるので、複素数の利便性がわかります。
例3
$$I = \int_0^{\infty} \frac{x^{m-1}}{1+x^n} dx, \quad (0<m<n, \text{\(m\), \(n\)は整数})$$
とか、
$$J = \int_{-\infty}^{\infty} \frac{\cos{x}}{x^4-1} dx$$
などの広義積分を計算するように言われた時、見た目は簡単でも、実際実数の範囲内だけで計算するとなると結構難しいです。
被積分関数が初等関数で書くことができずに、その広義積分を求める時、複素解析に置ける留数定理を使うと、一見計算できなさそうな広義積分もあっさりと計算できてしまいます。
それも複素数ならではの魅力です。
複素数の物理学への応用
物理学では、もともと物質、空間などの現実空間にある対象を物理法則を用いて解明していきます。
波動・振動論やFourier解析等は、Eulerの公式を用いることによって、複素数の利便性を発揮することができます。
しかし、本当に虚数という現実にない空間を使わなければ、この世界に起きている物理法則を解明することができないものがあります。
量子力学や素粒子物理学、宇宙物理学などミクロな世界を扱うとき、本当の意味で虚数が必要になってきます。
量子力学における複素数が現れるのは、運動量が量子力学では、\(- \hbar \nabla\)と表されたり、複素数を使ったHeisenbergの行列力学を用いることによって、運動量\(p\)と位置\(x\)を同時に正確に決定できないという有名なHeisenbergの不確定性原理（\(\Delta x \cdot \Delta p \geq \frac{\hbar}{2}\)）を導いたりと物理学、特にミクロな物理学では複素数は必須の概念となっています。
また、実在するかどうかはわかっていませんし、観測もできていませんが、光速を上回る空想上のエキセントリックな物質として複素数という質量を持った物質(タキオン)などを考えると、宇宙がなぜ加速膨張しているのか説明ができるらしいです。
まとめ
虚数や複素数がなぜ必要なのか、何の役に立つのか、数学や物理学で一体どのように使われているのかを具体例をあげながら説明しました。
この記事を機会に、身近に複素数という概念を感じられたら嬉しいと思います。