数独の解き方【上級編②】「X-wing（エックス-ウィング）」法

2018年8月19日2018年9月10日

数独の解き方（上級編）「X-wing（エックス-ウィング）」法

下図はとある数独の問題を解いている最中の図です。

実は、ここでとあるマスに数字が判明します。

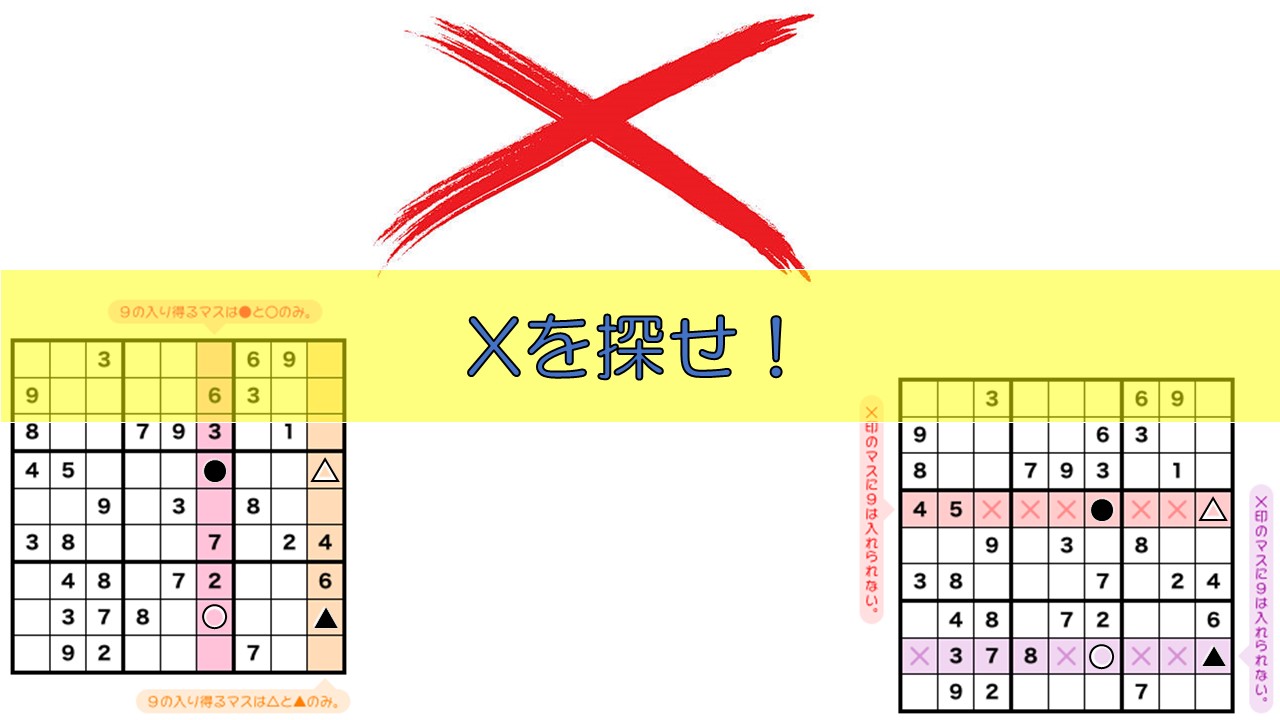
それを見つけるために、まずはピンク色とオレンジ色の２列に注目しましょう。

 

この２列において９の入り得るマスを探してみます。下図を見てください。

ピンク色の列では、●と○のどちらかに９が入ります。一方、オレンジ色の列では、△と▲のどちらかに９が入ります。

このように、●○▲△の４マスのうち２マスに９が入ることは簡単にわかりますね。

 

そして、●○▲△の４マスは長方形状に並んでいます。実は、ここがミソ！

同じヨコ列に同じ数字は入れられないということを考えると、２つの９の入れ方として「●と▲に入れる」「○と△に入れる」の２通りしかないことがわかります。

 

すると、どういうことが言えるのか。

その２通りのどちらであったとしても●と△のどちらか片方に必ず９が入るということが言えるんです。

ということは、下図の赤色ヨコ列において９の入り得るマスは●と△の２カ所に限定され、×印のマスには９が入れられないことがわかります。

同様に「○と▲のどちらか片方に必ず９が入る」とも言えるので、紫色ヨコ列についても×印のマスに９は入れられません。

 

それを踏まえた上で、赤色ヨコ列の★マス（下図）に注目します。

上記の解説により、★マスに９は入りません。

その上で★マスに入り得る数字を探すと……下の図の灰色マスを考慮すると１しか入れられないことが分かります。

これがX-wing法を使った数独の解き方です。

 

X-wing法を使うタイミングの判断としては、盤面に４〜６個ほど多めに現れている数字に着目して、その数字の入り得るマスを洗い出してみましょう。

「２カ所しか入らない列が２つあって、その４マスが矩形をなしている！」という場合、X-wing の手筋が使えるのではないかと考えてみましょう。

 

スポンサーリンク

なぜ、X-wing法と呼ばれるの？

ここで紹介した方法がなぜ「X-wing（エックス-ウィング）」法と呼ばれるのか？

それは、上記の解法の途中で示した図で説明できます。

説明の途中で以下の図が登場しましたね。

●に９が入るときは▲に９が入り、〇に９が入るときは△に９が入るということでした。

これを直線で結んでみると、

の青線のようになります。

Xの形になっていますね。これがX-wing法の名前の由来です。

このXをいかに見つけるかが、X-wing法を使いこなせるかに繋がります。

 

問題に挑戦しよう

ここでは「X-wing法」をマスターしました。

この方法を使って以下の問題に挑戦してみましょう！

[問題掲載予定]

 

スポンサーリンク

まとめ

• 数独の解き方（上級編）の二つ目としてX-wing法を紹介しました。
• ある数字が入る候補のマスがXの形（長方形の形）をしていれば、X-wing法を使用するチャンスです。

 

「数独の解き方【上級編③】「Swordfish（メカジキ）」法」へ進む↓

数独攻略へ戻る↓