【中学1年数学(一次方程式)】一次方程式の解き方 – 移項の本当の意味を理解すれば全部解ける!


- 一次方程式の解き方を丁寧に説明して欲しい
- 移項って何?勝手に項を移動させていいのはなぜ?
- 移項で符号が変わるのはなぜか知りたい
ここでは、中学校の1年生で習う一次方程式の解き方を丁寧に解説します。
まず、一次方程式とはどのような式のことをいうのかを復習します。
次に、方程式を解くためには”移項”という操作を行うのですが、移項という操作の本当の意味を理解しましょう。
難しくはありません。これをわかっていれば、計算に対する理解度がグンと上がりますよ!
このページを読み終えたとき、
- これでどんな一次方程式も解ける!
- 移項って本当はそんな意味だったんだ!だから、符号が変わるのか。
と必ず思ってもらえるはずです。
【動画解説】
※記事の内容はもっと詳しい説明となっていますので、記事にも目を通してみてくださいね。
一次方程式ってどんなヤツ?
まず、一次方程式とはどんな式のことをいうのかを復習しておきましょう。
そんなのは分かっているから、解き方から教えてっという人は次節の「一次方程式の解き方」まで移動をお願いします。
一次方程式とは、例えば以下のような式のことです。
- \(x = 1\)
- \(2a = 4\)
- \(10y = 4y – 11\)
- \(3b – 10 = b + 1\)
これらの式はすべて一次方程式です。
「なんとなくそうかなぁ」とわかるのではないでしょうか。
もう少しだけ、正確に説明しましょう。
「方程式」とはイコール(\(=\))で左右が繋がれていること、そして式中に文字があるもののことを言います。
また、「一次」とは式の中にある文字が1乗(例えば、\(x^1, a^1\))であることです。しかし、1乗は通常省略されますので、式中には\(x\)や\(a\)などと表現されます。
- \(=\)があり、文字がある。
- 文字は1乗である。1乗のことを一次ともいう。
スポンサーリンク
一次方程式の解き方
では、一次方程式を実際に解きながら、解き方をマスターしていきましょう。
次のような計算問題があったとします。
$$x + 7 = 3$$
この計算問題を解いて\(x\)は何かを求めてみましょう。
移項
ところで、一次方程式の解き方を学校で習うとき、必ず”移項”というワードが登場します。
移項とは、漢字が表しているように、
項を移す
という操作のことを言います。
項とは、足し算や引き算で繋がっている式を構成するもっとも細かい要素です(下の図を参照)。
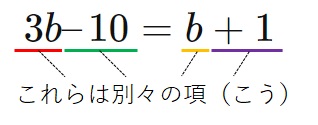
この項をイコールの逆側に移動させることが”移項”です。

では、
$$x + 7 = 3$$
を移項を使って解いてみます。
\(x\)を求めるためには、上の式を
$$x=\cdots$$
の形にしないといけないので、左辺の\(+7\)の項を右辺に移項すればよいでしょう。
なので、\(+7\)を右に持ってくるのですが、ここで移項をするときの重要なルールがあります。
それは、
移項したら、符号を逆にする
ということです。
なので、\(+7\)を移項すると、
\begin{align}
x + 7 &= 3 \\
x &= 3 – 7
\end{align}
となります。\(+\)が\(-\)変わっていますね。これを忘れないようにしましょう。
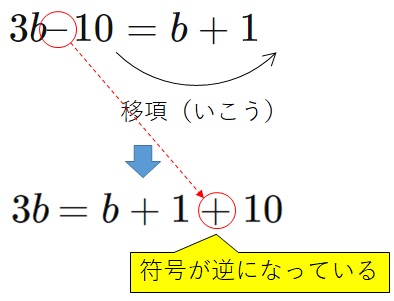
ということで、答えは、
\begin{align}
x + 7 &= 3 \\
x &= 3 – 7 \\
x &= -4 \\
\end{align}
ですね。
移項の本当の意味
移項をすると、符号が変わる
これは、機械的に覚えている人もいるかと思いますが、なぜそうなるのでしょうか?
移項の本当の意味がわかれば、計算しているときも自分が何をやっているのかが理解できるようになります。
すると、「計算するときに何をやっていいのか。」もしくは「何をやってはいけないのか」が判断できるようになるため、計算間違いも減っていきます。
移項で符号が変わるのは、結局、
方程式の\(=\)を常に成り立たせておくため
です。
例えば、先ほどの計算を例にとりましょう。
$$x + 7 = 3$$
この式は、左辺の\(x+7\)と右辺の\(3\)が等しいということを表しています。それがイコール(\(=\))の意味です。
ここで、イコールで結ばれている左右の数は等しいのですから、両辺から同じ数を引いても同じになるはずです。
$$10 = 10$$
という式があったとして、この式の両辺から\(1\)を引くと、
\begin{align}
10 – 1 &= 10 – 1\\
9 &= 9
\end{align}
という当たり前のことを言っています。
なので、\(x + 7 = 3\)の両辺から同じ数である\(7\)を引いてもいいはずです。
すると、
\begin{align}
x + 7 &= 3\\
x + 7 – 7 &= 3 – 7\\
x &= -4
\end{align}
となります。
上の式をよく見ると、下の図のように考えることができます。
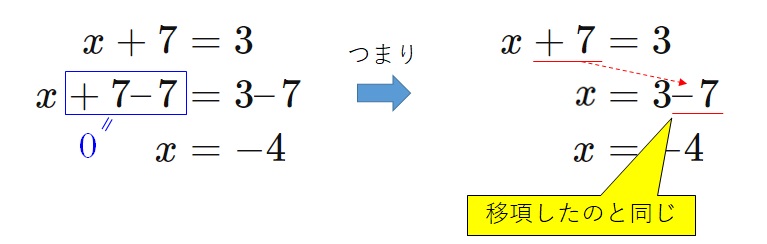
つまり、両辺から同じ数を引いた操作は、移項を行ったのと同じ操作をしていたということがわかります。
学校の勉強では、移項があまりにも当たり前になっているため、「両辺に同じ数を足したり引いたりして、\(x\)を求めていく」という考え方を知らない(もしくは忘れていた)人もいるかもしれません。
しかし、本来は、「両辺に同じ操作をして\(x\)を求める」という考え方が一番基礎にある考え方です。
その操作を見ると、あたかも項が移動しているように見えるため、便利で簡単な考え方として度導入されたのが”移項”という操作なのです。
掛け算や割り算も一緒
ここまでで、
”移項”とは、両辺に同じ数を足したり、引いたりすることと同じ意味
ということを学びました。
一次方程式を解くときは、足したり、引いたりするだけでなく、掛けたり割ったりもする必要があります。
次の計算問題を考えてみましょう。
\begin{align}
3 x = 12
\end{align}
これを解くには、両辺を\(3\)で割ればよいでしょう。すると、
\begin{align}
3 x &= 12\\
3 x \div 3 &= 12 \div 3\\
x &= 4
\end{align}
となり、答えは\(x=4\)となります。
つまり、これも両辺に同じ操作をして、左辺を\(x\)だけにしているのです。
移項が足し算・引き算だったのに対して、この場合は割り算を使ったというだけです。問題によっては掛け算を使う場合ももちろんあります。
スポンサーリンク
「一次方程式を解け」とはつまり…
ここまでの説明で結局何が言いたいのか。
それは、「一次方程式を解け」という問題は、
式の左右に同じ操作をして、\(x=\cdots\)の形にせよ。
ということを問われているのだ!と知って欲しかったのです。
そのために、
「両辺に同じ数だけ足したり、引いたり、掛けたり、割ったりしてもいいよ。」
「なぜなら、両辺はイコールで結ばれていて同じ数なんだから」
ということが分かっていれば、オッケーです。
私は、この考え方こそ、計算を行う上でもっとも大切な考え方の一つであると思っています。
ここで学んだことは今後数学を学んでいく上で、必ず役に立つでしょう。
計算を行うときはここで学んだことを思い出し「計算では何をしていいのか」、逆に「何をしてはいけないのか」をしっかりと意識しましょう。
そうすることで、計算に対する苦手意識が無くなり、計算間違いも少なくできます。
まとめ
一次方程式を解くために、”移項”という操作を使うことがありますが、これは方程式の両辺に同じ操作をした結果、項が移動して符号が変わっているように見えているだけ。
結局、「一次方程式を解け」とは、「両辺に同じ操作をして\(x=\dots\)の形を作れ」と同意。
計算の本質を知ることで、「やっていいこと」と「やってはいけないこと」が分かるようになる。
これが分かっていれば、計算間違いは劇的に減る!
























ディスカッション
コメント一覧
まだ、コメントがありません