【数学クイズ・パズル】正方形の一辺の辺の長さを求める数学パズル
数学パズルには、図形を使った問題が多くあります。
ここでは、「正方形の一辺の辺の長さを求める」問題を二問出題しましょう。
引っかけ問題ではありません。
柔軟に頭を働かせて解いていきましょう。難易度は「簡単～普通」レベルでしょうか。
数学パズル（第1問）
問題
さっそく問題です。
一辺が分かっていない正方形があります。
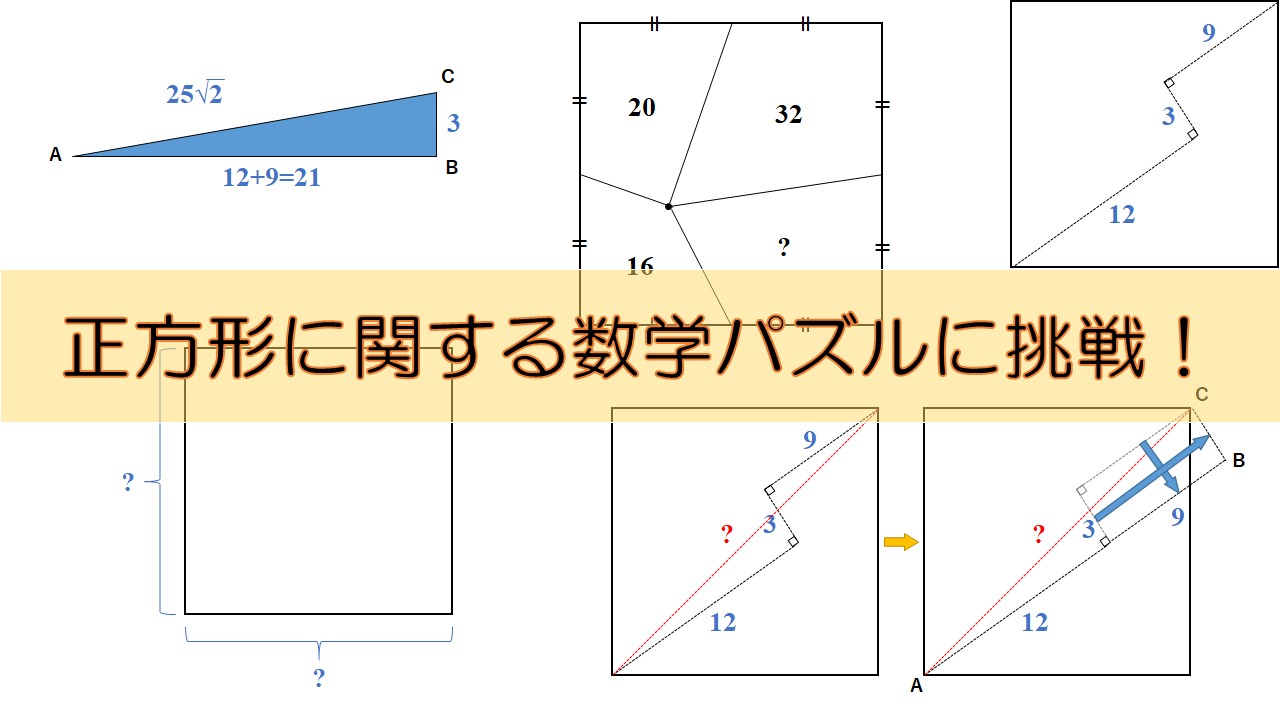
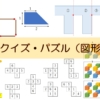
これを点線で示すように斜めに線を入れ、その長さを測ると以下のようになりました。
三つの点線の長さは、12, 3, 9であり、それぞれの直線は直角に接しています。
さて、この情報だけから正方形の一辺の長さを求めましょう。
まずは、ヒントなしで考えてみましょう。
「ちょっとヒントちょうだい！」という方に、以下にヒントを載せます。
ノーヒントで挑戦したいという方はスクロールし過ぎないように注意です。
ヒント
では、この数学パズルのヒントを出しましょう。
最終的に求めたいのは、正方形の一辺の長さです。
しかし、直接求めるのは無理そうです。
わかっているのは左下の角から右上の角まで引いた線の情報です。
ですので、なんとなく正方形の対角線に注目すれば良さそうです。
なので、まずは
正方形の対角線の長さ
を求めましょう。
対角線の長さがわかれば、あとは簡単に正方形の一辺の長さもわかりますよね。
解答
では、解答です。
ヒントで述べたように、対角線の長さを求めましょう。
そのために、点線を以下の図のように移動させます（青い矢印）。
すると、三角形ABCができました。
直線ABとBCは既にわかっています。
直線ACが正方形の対角線の長さになるため、これを三平方の定理で求めると、
\begin{align}
\text{ACの長さ} & = \sqrt{21^2 + 3^2} \\
& = \sqrt{450} \\
& = \sqrt{225 \times 2} \\
& = 15 \sqrt{2}
\end{align}
です。
これで正方形の対角線の長さが求まりました。
これから正方形の一辺の長さを求めるのは簡単ですね。
よって、答えは\(15\)です。
スポンサーリンク
数学パズル（第2問）
問題
次も正方形の一辺の長さを求める問題です。
またまた、一辺の長さがわかっていない正方形があります。
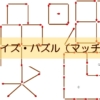
この正方形の各辺の中点から正方形内のある点まで、直線を引きました（下図）。
四つの領域ができましたが、そのうち三つの領域の面積がわかっています。一つの領域だけわかっていません。
情報はこれだけです。
ここからこの正方形の一辺の長さを求めましょう。
この問題は第1問目に比べると、少し難易度が高いです。
以下に、ヒントを示します。
だたし、そんなにヒントにならないヒントなので期待しないでください（笑）。
ヒント
4分割した領域の1領域だけ面積がわかっていないのは、その面積がわかっていれば正方形の面積がわかり、そこから以下の式を使って一辺の長さがわかるからです。
\begin{align}
\text{正方形の面積} & = \text{一辺の長さ}^2 \\
\text{一辺の長さ} & = \sqrt{\text{正方形の面積}}
\end{align}
ということで、わかっていない1領域の面積を求めることを目指しましょう。
ヒントは終わりです。
ヒントになってないかもしれませんが、ここから先を考えるのが醍醐味なので勘弁してください。
それでは考えてみましょう。
解答
では、解いていきましょう。
ヒントで言った通り、\(?\)で示された領域の面積を求めることを目指します。
そのために、補助線を以下の図の青い点線ように引きましょう。
ここで三角形ABOに注目し抜き出すと以下の図のようになります。
このとき三角形ABOを構成している三角形AMOとBMOの面積について考えてみましょう。
二つの三角形（AMOとBMO）の底辺をそれぞれAMとBMとすると、高さは以下のようになります。
高さは共通です。
そして、底辺であるAMとBMはいま長さが等しいですので、二つの三角形の面積は等しいということが分かります。
$$\text{三角形AMOの面積} = \text{三角形BMOの面積}$$
この面積を\(a\)としましょう。
他の辺についても同様に考えることができますので、それそれの三角形の面積の関係は以下の図のように表すことができます。
これより、以下の式が成り立つことが分かります。
\begin{align}
a + b & = 16 \tag{1} \\
b + c & = 20 \tag{2} \\
c + d & = 32 \tag{3} \\
d + a & = x \tag{4}
\end{align}
この式から\(x\)を求めていきます。
式(1)と式(3)を足すと、
$$a+b+c+d=16+32=48$$
です。
また、式(2)と式(4)を足すと、
$$b+c+d+a=20+x$$
です。
これら二つの式の左辺は\(a+b+c+d\)と共通ですので、以下の式が成り立ち、\(x\)が求まります。
\begin{align}
48 & = 20 + x \\
x & = 28
\end{align}
よって、正方形の面積が求まりました。
$$\text{正方形の面積} = 16 + 20 + 32 + 28 = 96$$
一辺の長さはこれの平方根をとればよいので、
$$\text{正方形の一辺の長さ} = \sqrt{96} = 4 \sqrt{6}$$
となります（答えがもっとキレイになるようにすればよかった…ゴメンナサイ）。
ここでは、正方形の面積に関する数学パズルを紹介しました。このように図形が登場する問題は色々なものがあります。他の問題も知りたいという人は以下のページにまとめているので覗いてみてくださいね↓
https://analytics-notty.tech/mathematics-quiz-puzzle-all-articles-summ...
まとめ
- 正方形に関する数学パズルを2問紹介しました
- 図形のパズル問題は補助線をうまく引くことで解き方のアイディアが生まれます