線を引くだけで掛け算ができてしまうスゴイ方法
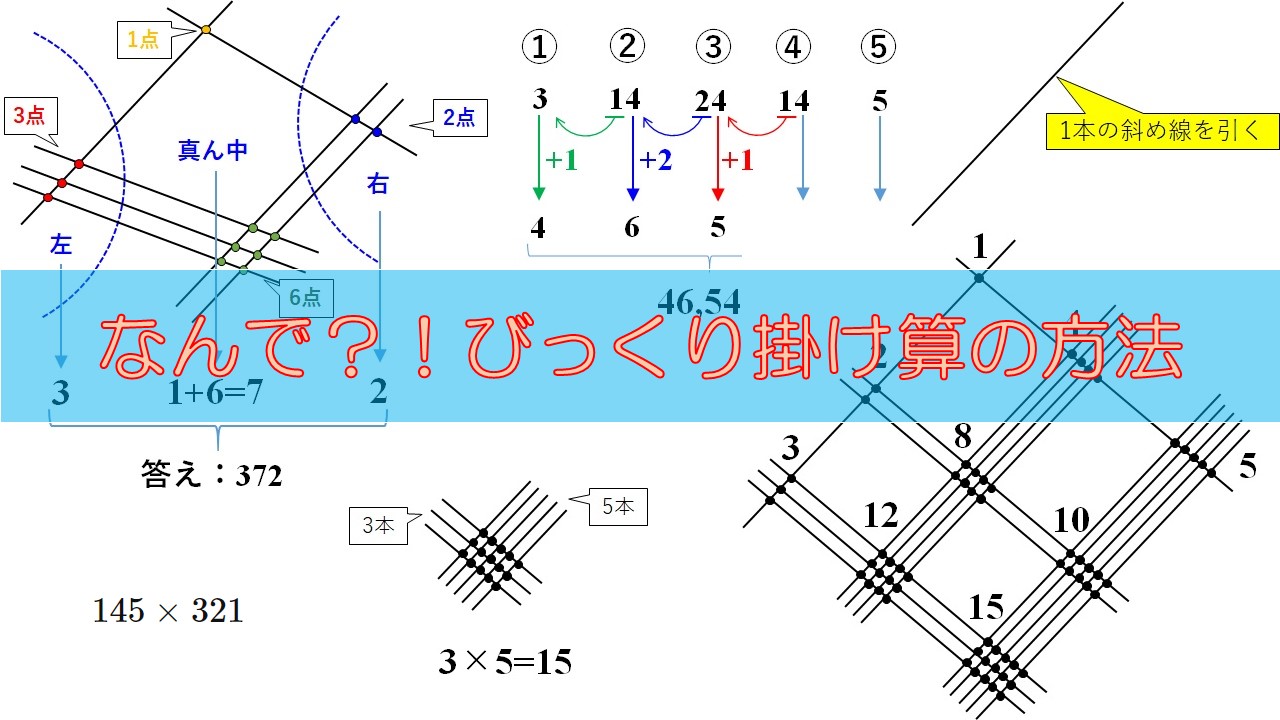
線を引くだけで簡単に掛け算ができてしまう方法を紹介します。
この方法は、もちろん2桁×2桁の掛け算くらいは簡単にできてしまいますし、3桁×3桁の掛け算すら簡単にできてしまうのです!
本当に、想像以上にスゴイ方法ですので必見ですよ!
線を引いて、点を数えるだけ
この掛け算の方法は本当に簡単です。その方法は、
線を引いて、点を数える。
これだけです!
そして、非常に強力です。
かなり難しい掛け算でもこの方法で比較的簡単に解けてしまうんです。
ただし、実際にテストなどの実践で使えるかと言われると、「普通の筆算をした方がいい」と答えざるえません。
あくまでもネタとして楽しんでください。すごく面白い方法ということだけは確かです。
ここから先は実際に掛け算を解いていきますが、できればみなさんも紙と鉛筆を準備して一緒にやってみましょう!
スポンサーリンク
2桁×2桁の掛け算の例
では、実際に掛け算の計算を行ってみましょう。
以下の2桁×2桁の計算問題にチャレンジです。
$$12 \times 31 =$$
まずは、掛け算の左側の数字に注目します。ここでは、\(12\)ですね。
この数字は、
- 十の位は\(1\)
- 一の位は\(2\)
です。
初めに、十の位の数である\(1\)に注目し、1本のラインを引きましょう。
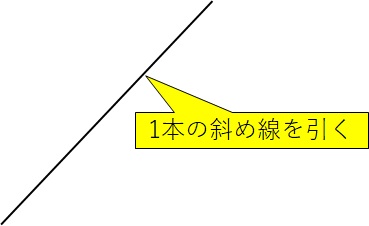
このように、右肩上がりの斜めの線を引くことがポイントです。
次に一の位の数字は2なので、2本の線を下の図のように引きます。
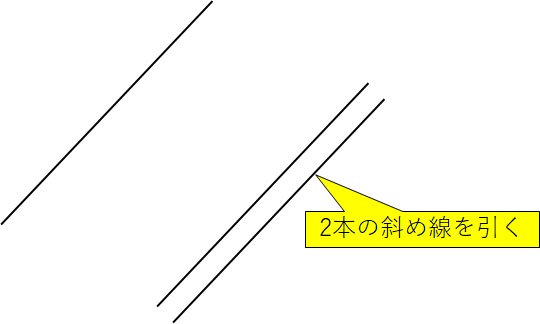
このように、初めに描いた線とは少し距離をとって、平行な線を描くことがポイントです。
続いて、掛け算の右側の数字に注目します。\(31\)でしたね。
この数字は、
- 十の位は\(3\)
- 一の位は\(1\)
です。
今度は、十の位は3なので、左下に右肩下がりの線を三本引きましょう。
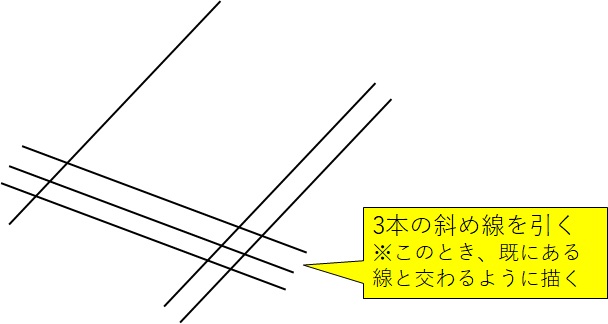
このとき、既に描いていた線と交わるように描かなければいけません。
そして、最後に一の位の1本を描きます。
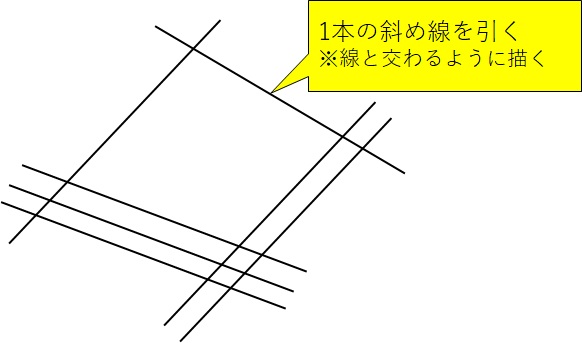
これで、線は完成です!
あとは、線と線が交わっている個数を数えていきましょう。
すると、下の図のようになるでしょう。

これを左、真ん中、右の3つのパートに分割します。
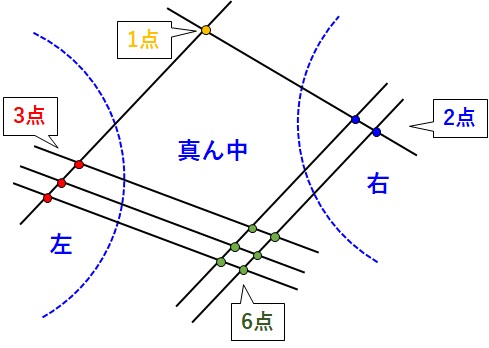
それぞれ、左、真ん中、右のパートで点の数を数えましょう。
- 左 → 3
- 真ん中 → 1 + 6 = 7
- 右 → 2
です。
最後に、この数字を並べてると、
$$372$$
となり、これが掛け算の答えとなります。
$$12 \times 31 = 372$$
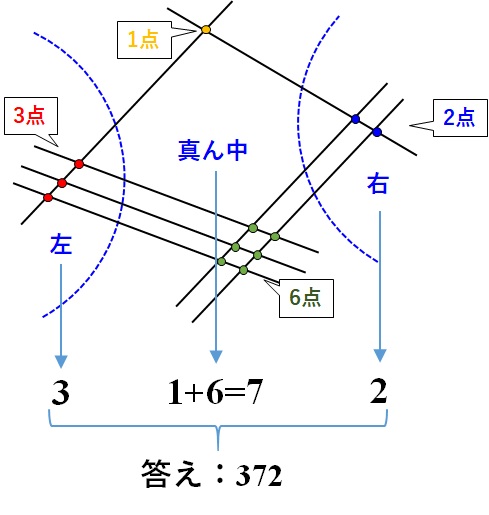
はじめなので長々と説明しましたが、簡単に覚えられるし、そんなに手間もかからないですよね。
こんな方法で掛け算ができるなんてすごいと思いませんか?!
繰り上がるときはどうするの?
では、同じようにして以下の掛け算を解いてみましょう。
$$21 \times 34$$
二回目なので、途中まではサクサク進めます。
まず、\(21\)の部分に対応する線を描いて、
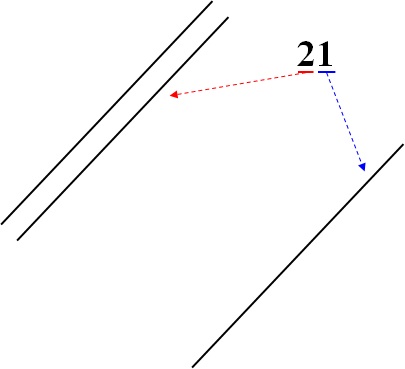
です。
次に、\(34\)の線を追加すると、
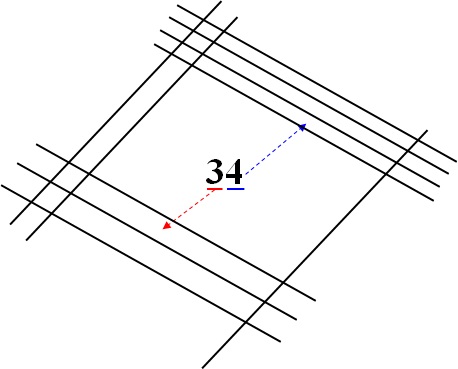
ですね。
そして、線と線が交わっている点を数えて、左、真ん中、右に分けると、下の図のようになります。
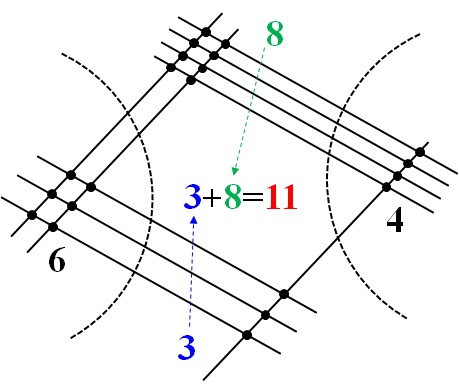
真ん中の数字の和が\(11\)となっており、2桁になってしまいました。
このような場合は、真ん中の数字の十の位(すなわち、ここでは\(11\)の\(1\))を左のパートへ渡すようにします。
つまり、\(1\)を左側の\(6\)に足します。
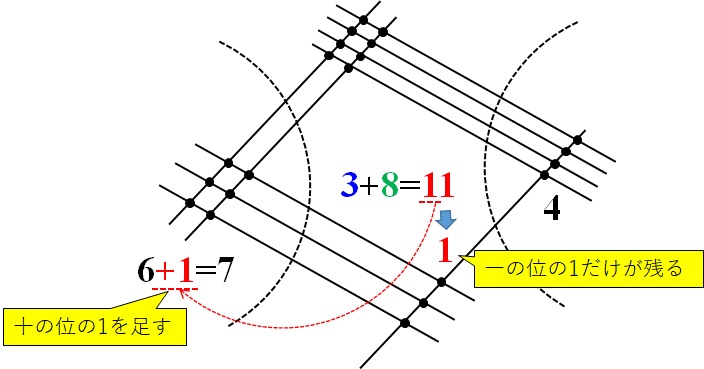
上の図のように、真ん中のパートの数は\(11\)から\(1\)になり、左のパートは\(6+1=7\)となります。
これで、各パートの数字が決まりました。
- 左 → \(7\)
- 真ん中 → \(1\)
- 右 → \(4\)
後はこれを左から並べて、
$$714$$
とすれば、これが答えです。
$$21 \times 34 = 714$$
このように、各パートに分けた数字が二桁になった場合は、一つ左のパートに十の位の数字を受け渡しましょう。
この問題の例では、真ん中の数字が2桁となりましたが、右のパートの数字が2桁になることもあります。その場合は、真ん中の数字に受け渡すのです。
ただし、一番左の数字が2桁になった場合は、受け渡すパートがありませんから、2桁のまま使ってしまってオッケーです。
練習問題
では、やり方をマスターしたところで、一問だけ練習問題をやってみましょう。
以下の掛け算を、ここで学んだ「線を引いて点を数える方法」で計算してみてください。
$$42 \times 24 = $$
以下に解答を載せます。
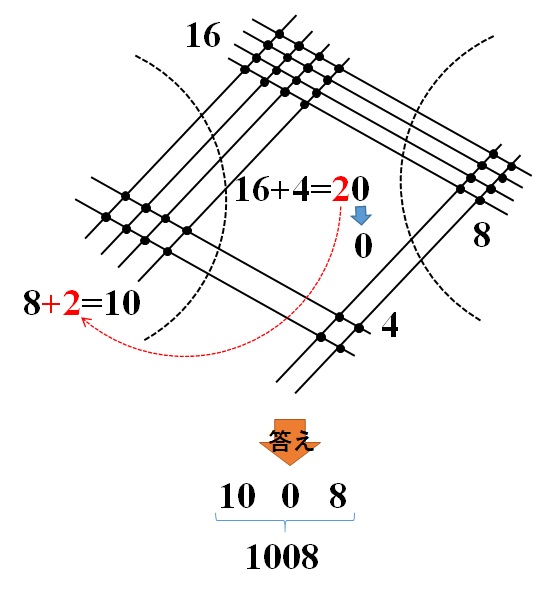
答えは、\(1008\)でした。できましたか?
スポンサーリンク
3桁×3桁の計算もできちゃう
もっと難しい問題にもチャレンジしてみましょう!
次の掛け算はどうでしょうか。
$$145 \times 321$$
まずは、\(145\)の線を描いてみます。今回は3桁ですので下の図のように三か所に線を集めて引きます。
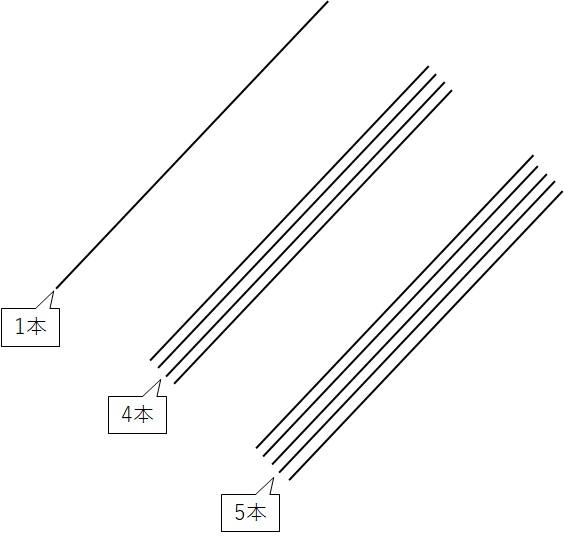
次は\(321\)ですね。下の図のようになります。

これで線は完成ですね。
次は、交点の数をかぞえていきましょう。
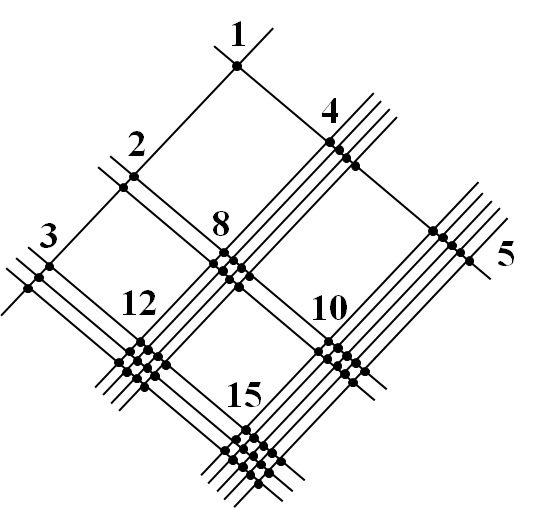
ここで、素直に点の数を数えていってもいいのですが、例えば一番下の\(15\)の部分などは数えるのが面倒です。
そんな場所は九九(くく)の掛け算に求めてしまいましょう。\(15\)の部分であれば、3本と5本の線が交わっているので、\(3 \times 5 = 15\)で簡単に求めることができますね(下の図を参照)。
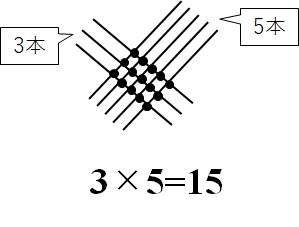
では、次はパート分割です。3桁×3桁の掛け算の場合は下の図のように①~⑤に分割します。
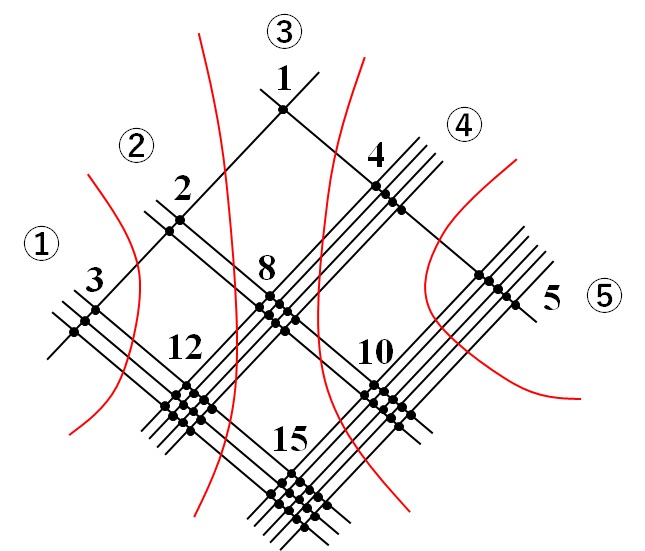
そして、各パートの数字を足します。
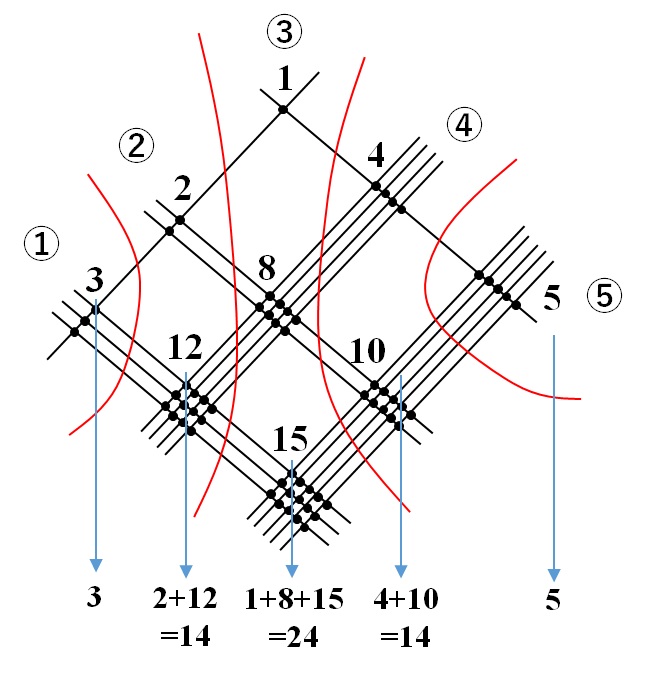
最後に、これらの数字を並べれば完成です。
ただし、十の位の数字を左に持っていく操作を忘れないでくださいね(下の図)。
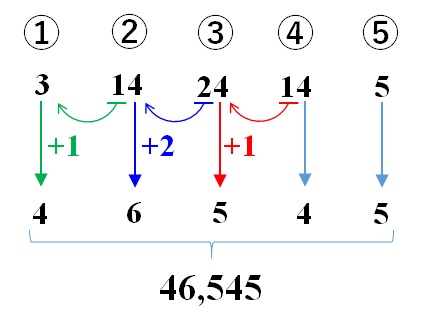
これが答えです。
問題の計算は\(145 \times 321\)でした。電卓でチェックしてみましょう。ちゃんと合ってますよね?
まとめ
線を引いてその点の数を数えるだけで掛け算ができる方法について紹介しました。
この方法はインド数学から生まれたとされています。
この記事では2桁×2桁と3桁×3桁を例題として解きましたが、4桁×4桁やもっと大きな桁数の掛け算も同じ方法で解けてしまいます。
すごく面白い方法でしたよね?
でも、残念ながら普通の筆算の方が計算スピードは速いと思います(笑)。
ネタとして披露すると、みんな驚くこと間違いないでしょう!


























ディスカッション
コメント一覧
まだ、コメントがありません