なぜ0の階乗は1（0!=1）なのか？

2018年8月26日2020年1月16日

この記事ではこんなことを紹介しています

学校の数学の授業で、

$$0!=1$$

$0$の階乗は$1$であることを知ります。

しかし、なぜそうなのかは教わりません。

「教科書にそう書いてあるから、とりあえず覚えてしまおう」と思った人が大半ではないでしょうか？

ここでは、「なぜ$0!=1$であるか」をいくつかのアプローチから丁寧に紹介していきます。

1. $0$の階乗はなぜ$1$なの？
2. 規則性を考えればその理由がわかる
3. 選び方の数から$0!$を考える
4. マクローリン展開の調和から考える
5. まとめ

$0$の階乗はなぜ$1$なの？

数学（高校？）で登場する”階乗”という数字の表現があります。

以下のような数です。

\begin{align}
& 3! \\
& 5! \\
& 10!
\end{align}

これらの計算は少し変わっていて、「数字を1ずつ減らしながら$1$になるまで掛けていく」という計算方法です。

つまり、

\begin{align}
& 3! = 3 \times 2 \times 1 = 6 \\
& 5! = 5 \times 4 \times 3 \times 2 \times 1 = 120 \\
& 10! = 10 \times 9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1 = 3628800
\end{align}

となります。

この計算を見て分かる通り、階乗の計算は少し数が大きくなるだけで、その計算した数はすぐにとんでもなく大きな数になってしまうという特徴があります。

$5!$は$120$だったのに、$10!$となると$300$万を超える数になっていますよね。

余談ですが、フランスのクリスティアン・クランプという数学者が階乗を研究していて、この急激な数の増加に驚いたため、ビックリマーク（正式名称：エクスクラメーションマーク）が階乗の記号に使われるようになったという歴史があります。

さて、この階乗についてですが、次の計算をしてください。

$$0!$$

$0$の階乗です。

これは、数学の授業で覚えたはずです。

答えは、

$$0! = 1$$

ですね。

$0$の階乗は$1$なんです。

数学で、なぜ$0$の階乗が$1$になるか疑問に思ったことはありませんか？

階乗は、「数字を1ずつ減らしながら$1$になるまで掛けていく」と学んだのに、この$0$だけは例外扱いなんです。

学生の私が感じていた違和感は、

「$1$の階乗も$1$で、値がかぶっているじゃん！」

「$0$の階乗はなんとなく$0$のような感じがする」

「負の数の階乗というものはないんだから、$0$の階乗も”ない”でいいじゃん」

ということでした。

こんな疑問はあったものの、習ったときは、何となく暗記して終わってしまいました。

しかし、きちんとした$0$の階乗が$1$である理由が知りたくて色々調べたのですが、

「やっぱり数学を発展させてきた先人達はスゴイ！」

という納得の理由がわかりましたので、ここにまとめておきたいと思います。

規則性を考えればその理由がわかる

$$0! = 1$$

である理由は複数あります。

まずは、中学の数学の知識でも簡単に納得できる理由から紹介しましょう。

それは、階乗した値の規則性に注目します。

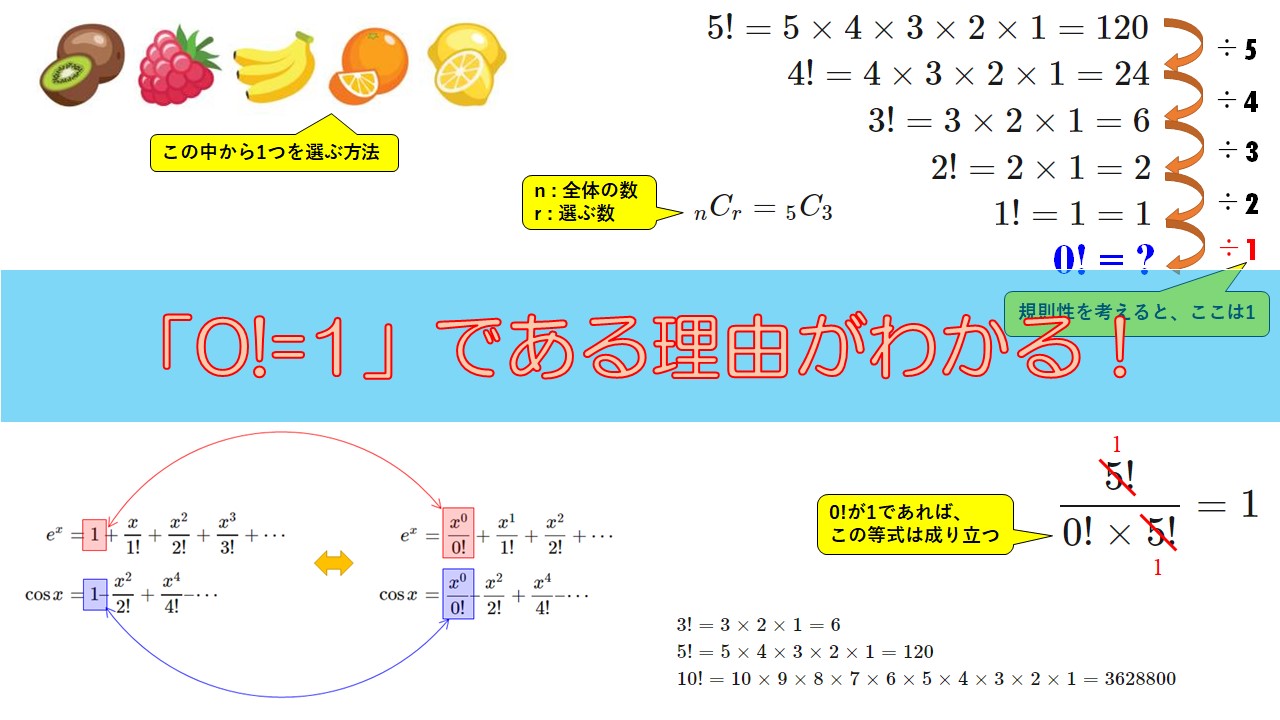
まずは、$1$から$5$までの階乗を数字が大きい方から並べてみましょう。

\begin{align}
5! = 5 \times 4 \times 3 \times 2 \times 1 = 120 \\
4! = 4 \times 3 \times 2 \times 1 = 24 \\
3! = 3 \times 2 \times 1 = 6 \\
2! = 2 \times 1 = 2 \\
1! = 1 = 1 \\
\end{align}

こうなります。

一番上の$5!$の$120$を、何で割れば$4!$の$24$になるでしょうか？

$$120 \div ? = 24$$

$?$は$5$ですね。$120$を$5$で割れば、$24$になります。

次に、$24$を何で割れば、その下の$6$になるでしょう？

$$24 \div ? = 6$$

これは$4$ですね。

このように、順番に考えていくと以下ようになります。

\begin{align}
120 \div ? = 24 \quad \rightarrow & \quad ?=5 \\
24 \div ? = 6 \quad \rightarrow & \quad ?=4 \\
6 \div ? = 2 \quad \rightarrow & \quad ?=3 \\
2 \div ? = 1 \quad \rightarrow & \quad ?=2
\end{align}

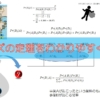
$?$は$5$から1ずつ減っていっていることが分かります。下の図を見た方がわかりやすいですね。

これは、階乗の性質を考えると当たり前のことなのですが、この規則性が$0$の階乗が$1$であることに繋がります。

では、$0$の階乗を以下の図から考えてみましょう。

割る数の規則的な減少から、$1!$から$0!$への割り算は$\div 1$であることがわかります。

それでは、上図の青い文字で書かれた$?$には何が入るでしょうか？

もうお分かりですね。

上の図から$1$を$1$で割った数が$0!$になるのですから、その答えは$1$となることが分かります。

このように、階乗の値の規則性から$0$の階乗は$1$にすべきことが分かります。

これが中学数学の範囲内でも説明できる、$0!$の階乗が$1$である理由でした。

選び方の数から$0!$を考える

次に、ものの選び方から$0!$を考える方法を紹介します。

この方法は高校数学の知識が必要ですが、そんなに難しいことはありません。

例えば、以下に5つの果物があります。

この中から、3つ選ぶ方法は何パターンあるでしょうか？

高校数学の基本的な数学問題で出てくるような問いですね。

こんな場合は、コンビネーションと呼ばれる記号$_nC_r$を使うと便利でした。

いまの問題のように5つの中から3つ選ぶときは、

$${ }_nC_r = { }_5C_3$$

のように書きます。

この計算は、以下のようになります。

$${ }_5C_3 = \frac{5 \times 4 \times 3}{3 \times 2 \times 1} = 10$$

よって、5つの中から3つ選ぶ方法は10通りということになります。

このように、${ }_nC_r$の計算は以下のように書けたことを思い出しましょう。

$${ }_nC_r = \frac{\frac{n!}{r!}}{ (n-r)!} = \frac{n!}{r! (n-r)!}$$

さて、では5つから1つを選ぶ方法は何通りあるでしょか？

上の式に$n$に$5$、$r$に$1$を代入して計算すればよいですから、

$${ }_5C_1 =\frac{5!}{1! (5-1)!} = 5$$

となり、答えは$5$通りです。

これは、直観的にも直ぐに5通りであることがわかりますね。

では、ここからが本題です。

「5つの中から0個選ぶ方法は何通りあるでしょう?」

まずは、直観的に考えてみましょう。

0個選ぶということは、”選ばない”ということです。

選ばないという選択肢は、明らかに1通りしかありません。

なので、上式の$n$に$5$を、$r$に$0$を代入したとき、この答えは1通りとなるはずです。

$${ }_5C_0 =\frac{5!}{0! (5-0)!} = 1$$

これを少し整理すると、

$$\frac{5!}{0! \times 5!} = 1$$

となります。

ここで$0!$が登場しました。

この等式を成立させるためには、$0!$はどんな値になればよいでしょうか？

それは明らかに$0! = 1$ですよね。

このように、いくつかのものから選ぶパターンの数を考えることによっても、$0!=1$とすれば都合がよいことがわかるのです。

マクローリン展開の調和から考える

ここからは、大学数学の知識が必要になります。

大学で基礎数学を学んだ方は”マクローリン展開”という公式を覚えていますか？

テイラー展開の方が有名ですので、こちらの方が聞き覚えがあるかもしれません。

マクローリン展開はテイラー展開のある特別な場合の公式です。

$e^x, \sin{x}, \cos{x}$数式で書くと以下のような形でした。

\begin{align}
e^x & = 1 + \frac{x}{1!} + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots \\
\sin{x} & = \frac{x}{1!} – \frac{x^3}{3!} + \frac{x^5}{5!} – \cdots \\
\cos{x} & = 1 – \frac{x^2}{2!} + \frac{x^4}{4!} – \cdots
\end{align}

これらを$k$（整数）を使って書くと、

\begin{align}
e^x & = \sum_{k=0}^{\infty} \frac{x^k}{k!} = \frac{x^0}{0!} + \frac{x^1}{1!} + \frac{x^2}{2!} + \cdots \\
\sin{x} & = \sum_{k=0}^{\infty} (-1)^k \frac{x^{2k+1}}{(2k+1)!} = \frac{x^1}{1!} – \frac{x^3}{3!} + \frac{x^5}{5!} – \cdots \\
\cos{x} & = \sum_{k=0}^{\infty} (-1)^k \frac{x^{2k}}{(2k)!} = \frac{x^0}{0!} – \frac{x^2}{2!} + \frac{x^4}{4!} – \cdots
\end{align}

となります。

この式と一つ前の式を見比べてみると、$e^x$と$\cos{x}$について、初めの$1$の部分の表現に$0!$をどう定義するかが重要であることが分かります。