不思議で面白い数字の雑学・トリビア10選

2018年1月17日2020年5月19日

使えないけど面白い数字の雑学・トリビアを紹介

面白い数字の不思議で面白い雑学・トリビアについて紹介します。

このサイト全体が数字・数学のトリビアに関して紹介していますが、その中でも

• 面白いけど生活や勉強には使えなさそう
• 短い説明でも分かるし簡単

というものを10つ選びました。

役には立たないかもしれないですが、絶対に人に話したくなること間違いなしですよ！

 

スポンサーリンク

①円周率3.14の秘密

円周率は数学で一番有名な定数かもしれません。学校では、その値は3.14と習いますね。

ところで、円周率は\(π\)（パイ）と呼び、同じ発音で円の形をした食べ物にパイ（アップルパイなど）がありますよね。

英語表記だと、

PIE

と書きます。

この”PIE”と”3.14″にはある秘密があります。

“3.14”を左右に反転してください。

すると…なんと”PIE”の文字が現れました！（下の画像）

詳しくはこちら↓

 

②11,111×11,111の答えが美しい

1が連続した数同士の掛け算、例えば、

$$11,111 \times 11,111$$

の答えは、

$$11,111 \times 11,111 = 123,454,321$$

となります。数字に対称性が現れましたね。

これ以外にも、1が連続した数同士の掛け算、

\begin{align}
1 & \times 1 \\
11 & \times 11 \\
111 & \times 111 \\
& \cdots \\
111,111,111 & \times 111,111,111
\end{align}

の答えは美しい対称性を持ちます。なぜこのような答えになるかは筆算を考えれば理解しやすいです。

詳しくはこちらをご覧ください↓

 

スポンサーリンク

③6と9を使って答えも6と9にする

簡単です。6と9を掛けた数と6と9を足した数を足すと、答えも6と９を使って書けるというものです。

こんな感じです。

$$(6 \times 9) + (6 + 9) = 69$$

要は、式全部が6と9を使って書けるよって話です。

ちょっと物足りないですかね。

 

④マジックナンバー”142857″

一見、特に変わった特徴のない数字にみえる”142857″ですが、実は面白い性質をたくさん持った数なのです。

例えば、この数字に1から6までの数字を掛けてみましょう。

\begin{align}
142857 \times 1 & = 142857 \\
142857 \times 2 & = 285714 \\
142857 \times 3 & = 428571 \\
142857 \times 4 & = 571428 \\
142857 \times 5 & = 714285 \\
142857 \times 6 & = 857142
\end{align}

お気づきでしょうか？

答えに使われている数字はすべて同じです。しかも同じ順番で数字が循環していることがわかります。

さらに、7も掛けてみましょう。

\begin{align}
142857 \times 7 = 999999
\end{align}

9が並びました。

ここで紹介した以外にも、”142857″には面白い性質がたくさんあります。詳しくは、

をご覧ください。

 

スポンサーリンク

⑤1から10まですべての数で割れる最小の数字は？

2520

誰が見つけたのかわかりませんが、この数字、

1, 2, 3, 4, 5, 6, 7, 8, 9, 10

のすべての数字で割ることができる最小の数なんです。

実際に電卓で割って確かめてみると、

\begin{align}
2520 \div 1 & = 2520 \\
2520 \div 2 & = 1260 \\
2520 \div 3 & = 840 \\
2520 \div 4 & = 630 \\
2520 \div 5 & = 504 \\
2520 \div 6 & = 420 \\
2520 \div 7 & = 360 \\
2520 \div 8 & = 315 \\
2520 \div 9 & = 280 \\
2520 \div 10 & = 252 \\
\end{align}

となり、ちゃんとすべての数で割ることができました。

 

⑥9で割り切れるかを一瞬で判断する

下の数字をご覧ください。

$$192834$$

この数字は9で割り切れると思いますか？五秒で答えてください。電卓を使うのはなしです。

普通に計算するととても五秒では無理ですよね。

しかし、ある方法を使うと数秒で9で割り切れるかが分かってしまいます。それは、

数字の各桁をすべて足すのです。こうなります。

$$1+9+2+8+3+4=27$$

さらに、数字の各桁の数字を足します。

$$2+7=9$$

“9”になりましたね。このように、各桁を足していって最後に”9″になると元の数(192834)は”9で割り切れる数”というふうに言えます。

 

では、

$$116$$

はどうでしょうか？

各桁の合計は8ですね。なので、116は9では割り切れない数ということになります。

ここで注目した数”9″は不思議な数字です。以下の記事にまとめてますので、ぜひご覧ください。

 

⑦割って割って元の数に戻っちゃう？

適当な三桁の数字を思い浮かべてください。私は、

$$349$$

を思い浮かべました。

この数を二回書きます。

$$349349$$

この数を三つの素数(7, 11, 13)で割ってしまいましょう。すると、

$$349349 \div 7 \div 11 \div 13 = 349$$

出てきた数は”349″です。

あれっ！元の数に戻ってしまいました。詳しくは、以下の記事で！

 

⑧”496″は神秘の数字

“496”は宇宙の真理を表す数だと言われています。

“496”を割り切ることのできる数を列挙してみましょう。それは、

$$1, 2, 4, 8, 16, 31, 62, 124, 248$$

では、これらの数字をすべて足します。

$$1+2+4+8+16+31+62+124+248=496$$

元の数”496″になりましたね。

これは、完全数という数で、

自分の約数（割り切ることのできる数）をすべて足すと、自分自身の数に戻ってしまう

のような性質があります。

完全数は”496″以外にもたくさんあるのですが、”496″はその他にも色々な面白い性質・現象がたくさんあるのです。

そのため、”宇宙の真理を表す数”とされています。

 

⑨カプレカ数

カプレカ数という不思議な数字が存在します。その数字は、

$$495$$

です。

一体どんな性質を持った数なのでしょう。

まずは、適当な三桁の数字を思い浮かべてください。ただし、すべて同じ数はダメです。

ここでは、

$$824$$

を選びました。

まず、この数の各桁を大きい数字から並べかえましょう。すると、

$$824 \rightarrow 842$$

となります。さらに、小さい方から並べた数も用意します。

$$824 \rightarrow 248$$

そして、大きいほうの数から小さい方の数を引きます。

$$842 – 248 = 594$$

出てきた数をさらに同じように並び替え引き算します。

$$954 – 459 = 495$$

ここで、始めに紹介したカプレカ数”495″が登場しましたね。

さらに、同じ操作を続けます。

$$954 – 459 = 495$$

あれ！数が変わりません。これでおしまいですね。

 

実は、三桁のどんな数（ただしすべて同じ数字はダメ）を選んでも、最終的にはこのカプレカ数”495″に行き着くのです。

他の数字でも試してみてくださいね。

 

ちなみに、ここでは三桁のカプレカ数を紹介しましたが、四桁のカプレカ数もあります。

カプレカ数に興味が沸いてきた方は、以下の記事をどうぞ。

 

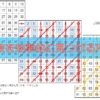
⑩すべて同じ曜日の日

数字の雑学・トリビアではないかもしれませんが、カレンダーには面白い性質が潜んでいます。

可能であれば、次の日付が何曜日であるかを調べてみてください。何年のカレンダーでもよいですよ。

4/4、6/6、8/8、10/10、12/12

どうでしたか？

ちなみに、2018年はすべて水曜日です。

年によって曜日は違いますが、一年の間ではすべて同じ曜日となるのです。

 

まとめ

• 面白くて不思議な性質を持った数字はたくさんある
• 数字や数学が好きな人はこのサイトを楽しんでね